Question Number 124682 by mathocean1 last updated on 05/Dec/20
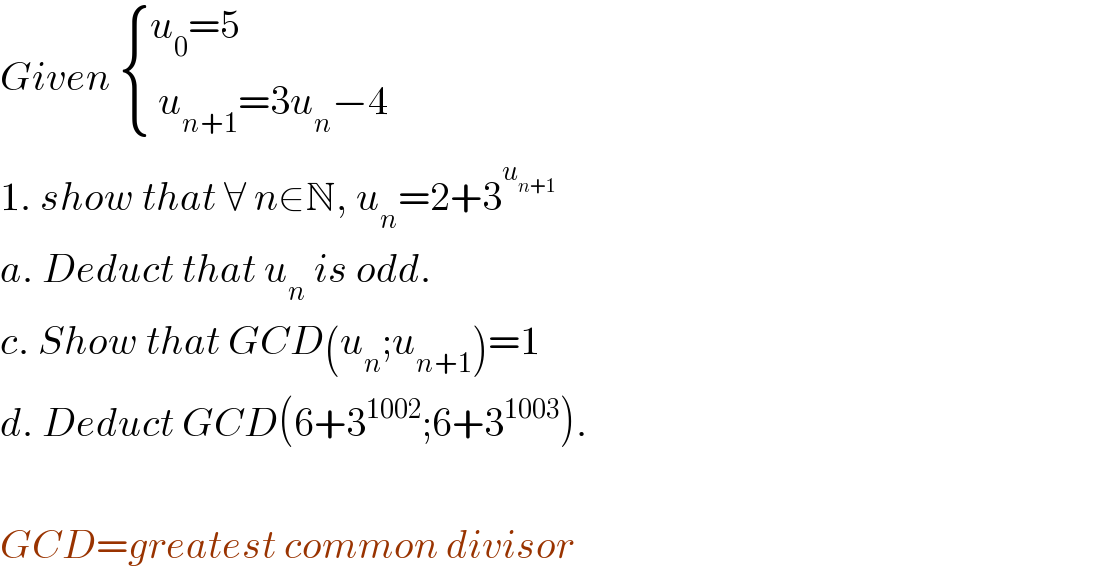
$${Given}\:\begin{cases}{{u}_{\mathrm{0}} =\mathrm{5}}\\{\:{u}_{{n}+\mathrm{1}} =\mathrm{3}{u}_{{n}} −\mathrm{4}}\end{cases} \\ $$$$\mathrm{1}.\:{show}\:{that}\:\forall\:{n}\in\mathbb{N},\:{u}_{{n}} =\mathrm{2}+\mathrm{3}^{{u}_{{n}+\mathrm{1}} } \:\:\: \\ $$$${a}.\:{Deduct}\:{that}\:{u}_{{n}} \:{is}\:{odd}. \\ $$$${c}.\:{Show}\:{that}\:{GCD}\left({u}_{{n}} ;{u}_{{n}+\mathrm{1}} \right)=\mathrm{1} \\ $$$${d}.\:{Deduct}\:{GCD}\left(\mathrm{6}+\mathrm{3}^{\mathrm{1002}} ;\mathrm{6}+\mathrm{3}^{\mathrm{1003}} \right). \\ $$$$ \\ $$$${GCD}={greatest}\:{common}\:{divisor}^{} \\ $$
