Question Number 166954 by cortano1 last updated on 03/Mar/22
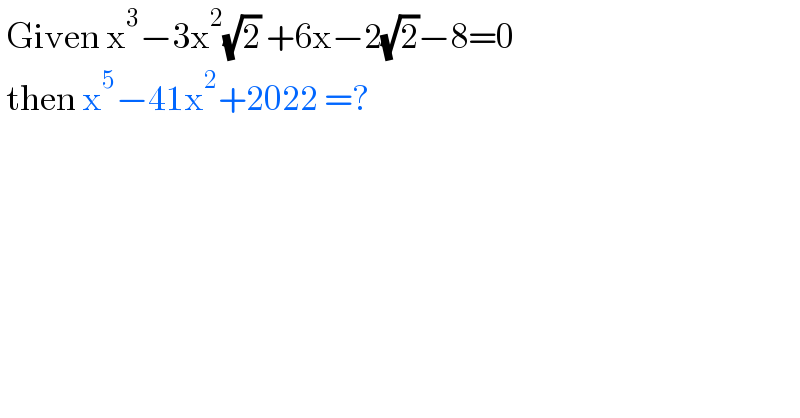
$$\:\mathrm{Given}\:\mathrm{x}^{\mathrm{3}} −\mathrm{3x}^{\mathrm{2}} \sqrt{\mathrm{2}}\:+\mathrm{6x}−\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{8}=\mathrm{0} \\ $$$$\:\mathrm{then}\:\mathrm{x}^{\mathrm{5}} −\mathrm{41x}^{\mathrm{2}} +\mathrm{2022}\:=? \\ $$
Answered by som(math1967) last updated on 03/Mar/22
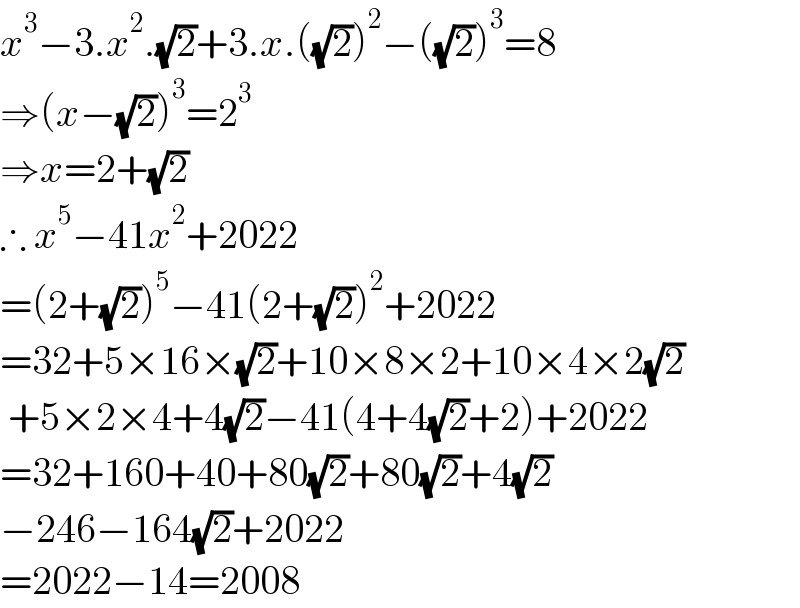
$${x}^{\mathrm{3}} −\mathrm{3}.{x}^{\mathrm{2}} .\sqrt{\mathrm{2}}+\mathrm{3}.{x}.\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{8} \\ $$$$\Rightarrow\left({x}−\sqrt{\mathrm{2}}\right)^{\mathrm{3}} =\mathrm{2}^{\mathrm{3}} \\ $$$$\Rightarrow{x}=\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\therefore\:{x}^{\mathrm{5}} −\mathrm{41}{x}^{\mathrm{2}} +\mathrm{2022} \\ $$$$=\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{5}} −\mathrm{41}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{2022} \\ $$$$=\mathrm{32}+\mathrm{5}×\mathrm{16}×\sqrt{\mathrm{2}}+\mathrm{10}×\mathrm{8}×\mathrm{2}+\mathrm{10}×\mathrm{4}×\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:+\mathrm{5}×\mathrm{2}×\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{41}\left(\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}}+\mathrm{2}\right)+\mathrm{2022} \\ $$$$=\mathrm{32}+\mathrm{160}+\mathrm{40}+\mathrm{80}\sqrt{\mathrm{2}}+\mathrm{80}\sqrt{\mathrm{2}}+\mathrm{4}\sqrt{\mathrm{2}} \\ $$$$−\mathrm{246}−\mathrm{164}\sqrt{\mathrm{2}}+\mathrm{2022} \\ $$$$=\mathrm{2022}−\mathrm{14}=\mathrm{2008} \\ $$
