Question Number 109577 by bemath last updated on 24/Aug/20
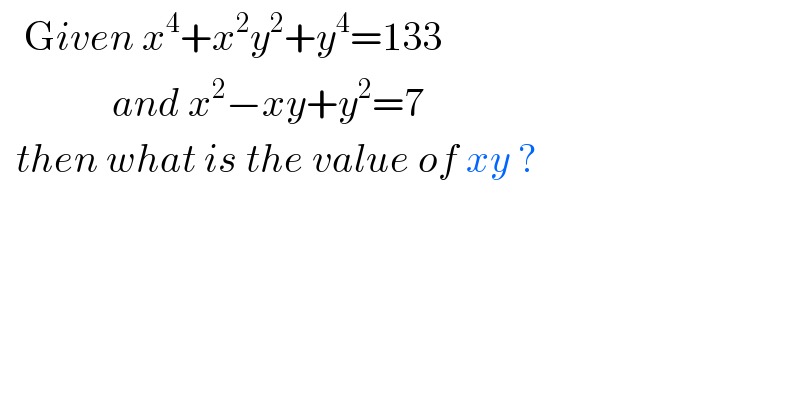
$$\:\:\:\mathrm{G}{iven}\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} =\mathrm{133} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:{and}\:{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{7} \\ $$$$\:\:{then}\:{what}\:{is}\:{the}\:{value}\:{of}\:{xy}\:? \\ $$
Commented by bemath last updated on 24/Aug/20

$${cooll}….. \\ $$
Answered by Dwaipayan Shikari last updated on 24/Aug/20
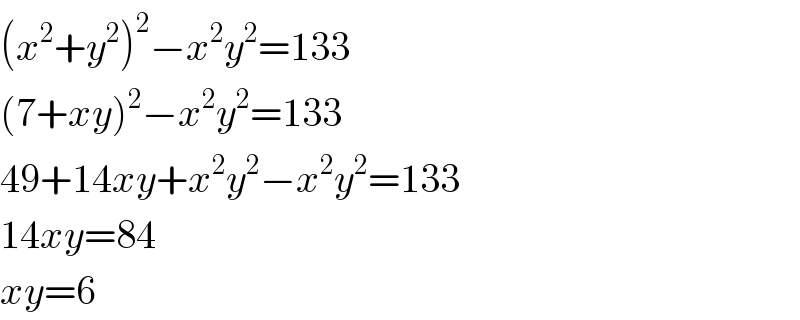
$$\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{133} \\ $$$$\left(\mathrm{7}+{xy}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{133} \\ $$$$\mathrm{49}+\mathrm{14}{xy}+{x}^{\mathrm{2}} {y}^{\mathrm{2}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{133} \\ $$$$\mathrm{14}{xy}=\mathrm{84} \\ $$$${xy}=\mathrm{6} \\ $$
Answered by john santu last updated on 24/Aug/20
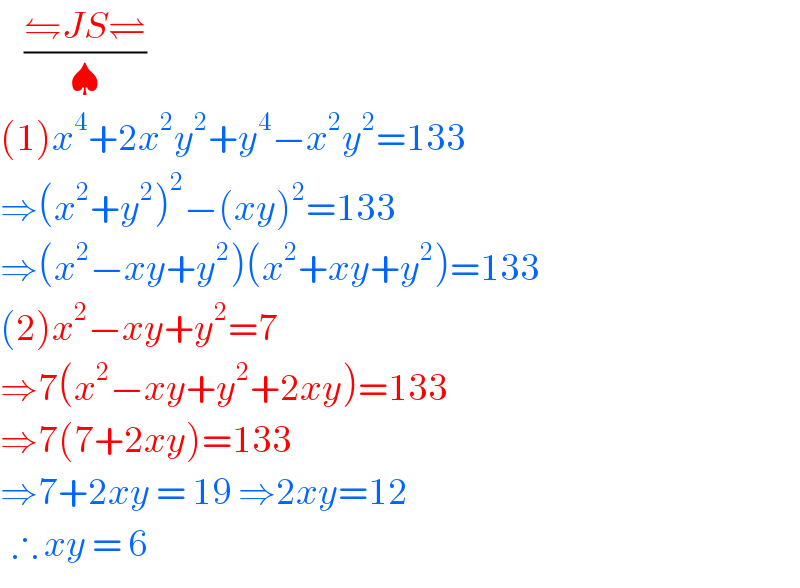
$$\:\:\:\:\frac{\leftrightharpoons{JS}\rightleftharpoons}{\spadesuit} \\ $$$$\left(\mathrm{1}\right){x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} −{x}^{\mathrm{2}} {y}^{\mathrm{2}} =\mathrm{133} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} −\left({xy}\right)^{\mathrm{2}} =\mathrm{133} \\ $$$$\Rightarrow\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)=\mathrm{133} \\ $$$$\left(\mathrm{2}\right){x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{7} \\ $$$$\Rightarrow\mathrm{7}\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} +\mathrm{2}{xy}\right)=\mathrm{133} \\ $$$$\Rightarrow\mathrm{7}\left(\mathrm{7}+\mathrm{2}{xy}\right)=\mathrm{133}\: \\ $$$$\Rightarrow\mathrm{7}+\mathrm{2}{xy}\:=\:\mathrm{19}\:\Rightarrow\mathrm{2}{xy}=\mathrm{12} \\ $$$$\:\:\therefore\:{xy}\:=\:\mathrm{6} \\ $$
Commented by mnjuly1970 last updated on 24/Aug/20

Answered by Rasheed.Sindhi last updated on 24/Aug/20
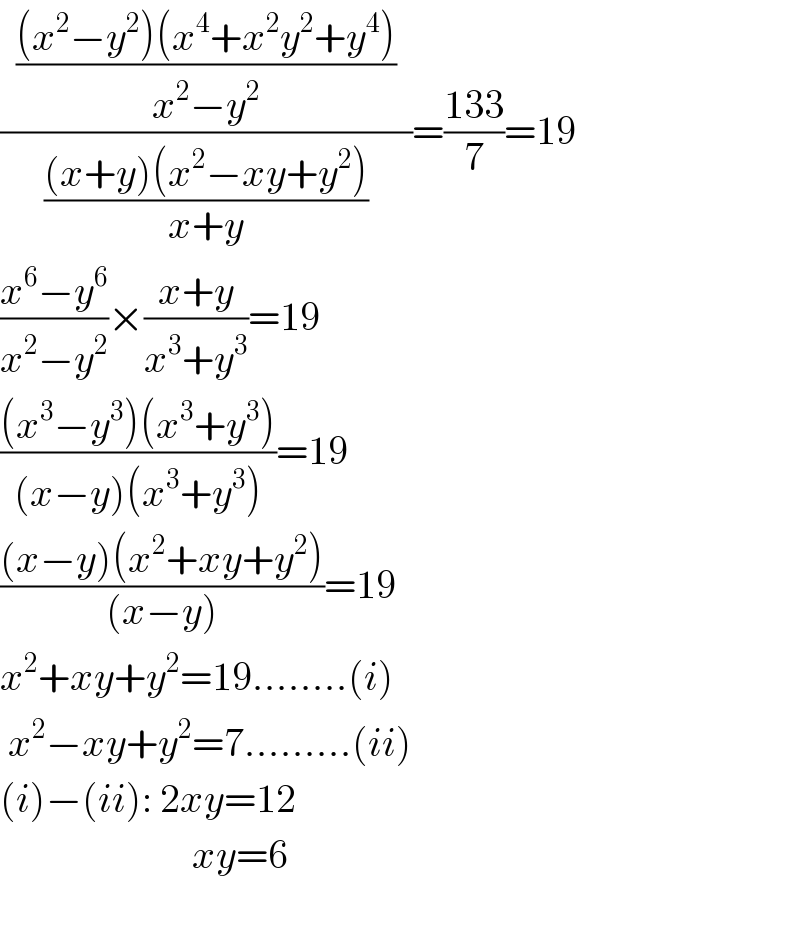
$$\frac{\:\:\frac{\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} \right)}{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }\:\:}{\frac{\left({x}+{y}\right)\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)}{{x}+{y}}}=\frac{\mathrm{133}}{\mathrm{7}}=\mathrm{19} \\ $$$$\frac{{x}^{\mathrm{6}} −{y}^{\mathrm{6}} }{{x}^{\mathrm{2}} −{y}^{\mathrm{2}} }×\frac{{x}+{y}}{{x}^{\mathrm{3}} +{y}^{\mathrm{3}} }=\mathrm{19} \\ $$$$\frac{\left({x}^{\mathrm{3}} −{y}^{\mathrm{3}} \right)\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)}{\left({x}−{y}\right)\left({x}^{\mathrm{3}} +{y}^{\mathrm{3}} \right)}=\mathrm{19} \\ $$$$\frac{\left({x}−{y}\right)\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)}{\left({x}−{y}\right)}=\mathrm{19} \\ $$$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{19}……..\left({i}\right) \\ $$$$\:{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{7}………\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right):\:\mathrm{2}{xy}=\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{xy}=\mathrm{6} \\ $$$$ \\ $$
Answered by Rasheed.Sindhi last updated on 24/Aug/20
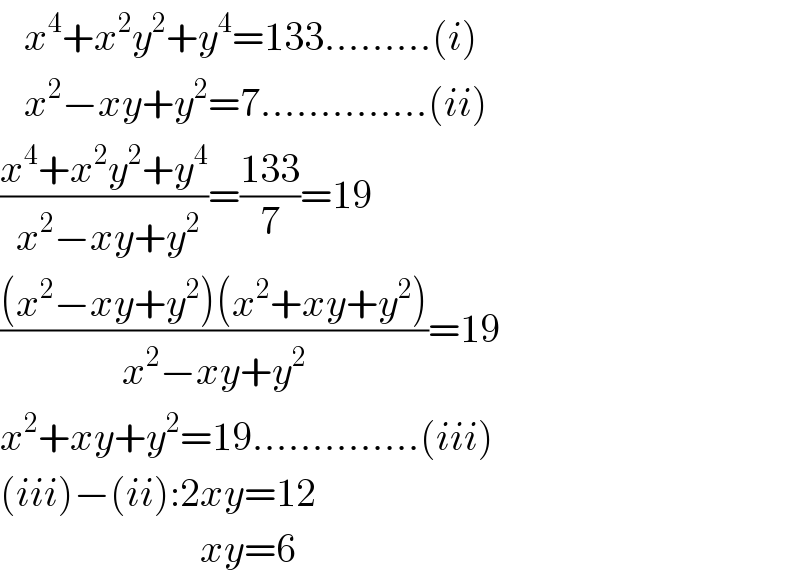
$$\:\:\:{x}^{\mathrm{4}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} =\mathrm{133}………\left({i}\right) \\ $$$$\:\:\:{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} =\mathrm{7}…………..\left({ii}\right) \\ $$$$\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} }{\:{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} }=\frac{\mathrm{133}}{\mathrm{7}}=\mathrm{19} \\ $$$$\frac{\left({x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} −{xy}+{y}^{\mathrm{2}} }=\mathrm{19} \\ $$$${x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{19}…………..\left({iii}\right) \\ $$$$\left({iii}\right)−\left({ii}\right):\mathrm{2}{xy}=\mathrm{12} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{xy}=\mathrm{6} \\ $$
