given-x-ln-34-y-ln-38-find-ln-32-in-terms-of-x-and-y-

Question Number 103766 by bramlex last updated on 17/Jul/20

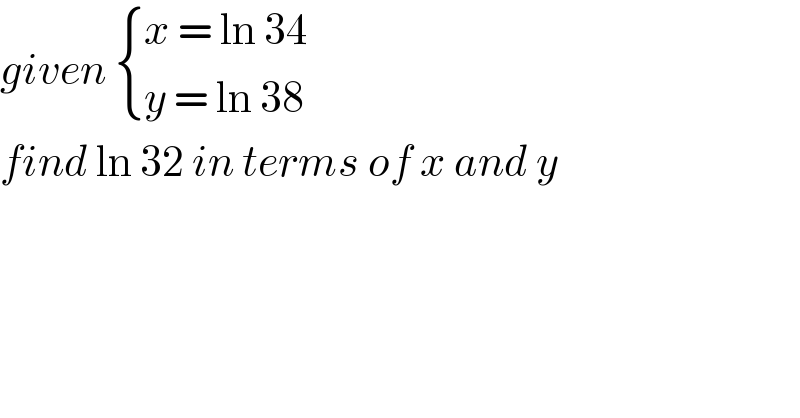
g i v e n {\begin{cases} x = \ln 34 \\ y = \ln 38 \end{cases}

f i n d \ln 32 i n t e r m s o f x a n d y

Answered by Dwaipayan Shikari last updated on 17/Jul/20

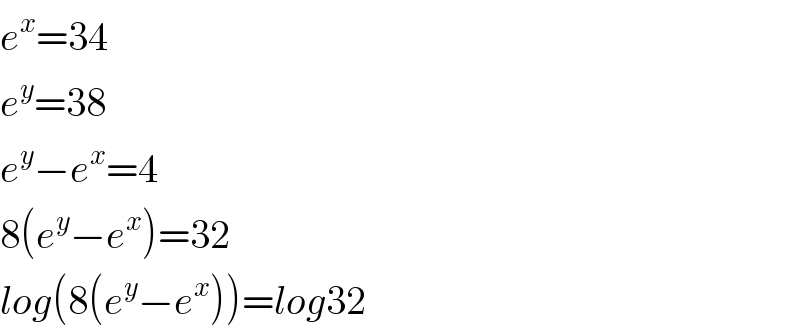
e^{x} = 34

e^{y} = 38

e^{y} - e^{x} = 4

8 (e^{y} - e^{x}) = 32

l o g (8 (e^{y} - e^{x})) = l o g 32