Question Number 170415 by Mastermind last updated on 23/May/22
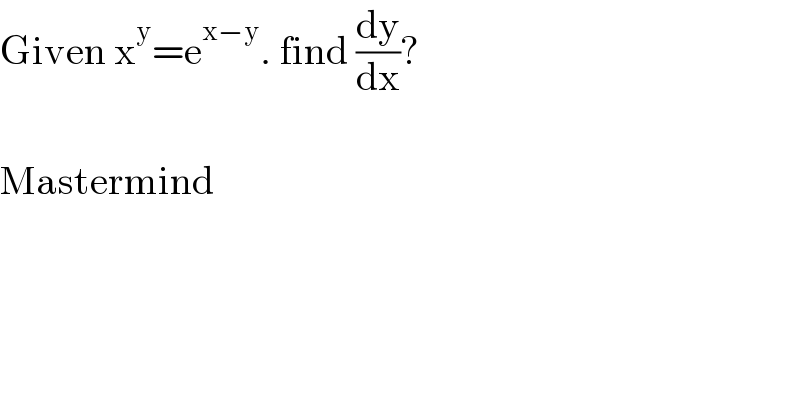
$$\mathrm{Given}\:\mathrm{x}^{\mathrm{y}} =\mathrm{e}^{\mathrm{x}−\mathrm{y}} .\:\mathrm{find}\:\frac{\mathrm{dy}}{\mathrm{dx}}? \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$
Answered by aleks041103 last updated on 23/May/22
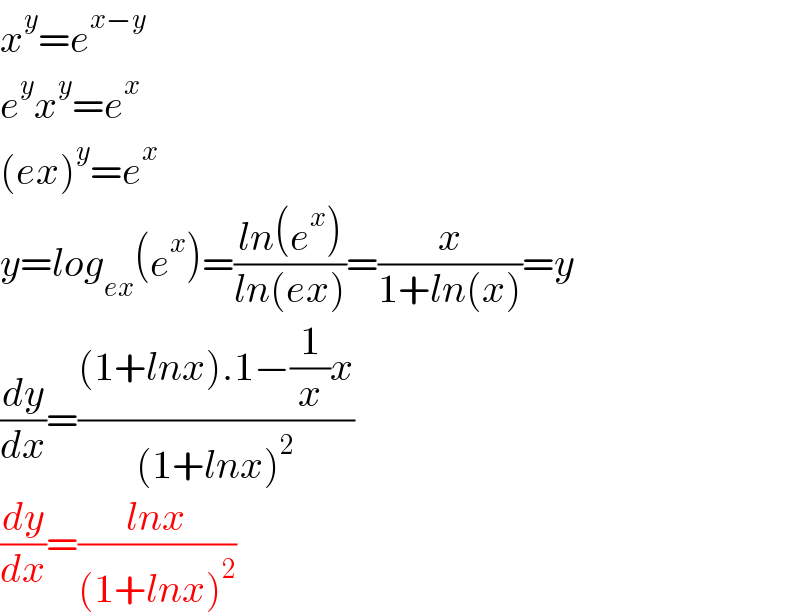
$${x}^{{y}} ={e}^{{x}−{y}} \\ $$$${e}^{{y}} {x}^{{y}} ={e}^{{x}} \\ $$$$\left({ex}\right)^{{y}} ={e}^{{x}} \\ $$$${y}={log}_{{ex}} \left({e}^{{x}} \right)=\frac{{ln}\left({e}^{{x}} \right)}{{ln}\left({ex}\right)}=\frac{{x}}{\mathrm{1}+{ln}\left({x}\right)}={y} \\ $$$$\frac{{dy}}{{dx}}=\frac{\left(\mathrm{1}+{lnx}\right).\mathrm{1}−\frac{\mathrm{1}}{{x}}{x}}{\left(\mathrm{1}+{lnx}\right)^{\mathrm{2}} } \\ $$$$\frac{{dy}}{{dx}}=\frac{{lnx}}{\left(\mathrm{1}+{lnx}\right)^{\mathrm{2}} } \\ $$
