Question Number 115733 by bemath last updated on 28/Sep/20
$${Given}\:{xy}\:=\frac{\mathrm{1}}{\mathrm{3}}\:{for}\:{x},{y}\in\mathbb{R}\: \\ $$$${find}\:{min}\:{value}\:{of}\:\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\frac{\mathrm{9}}{{y}^{\mathrm{6}} } \\ $$
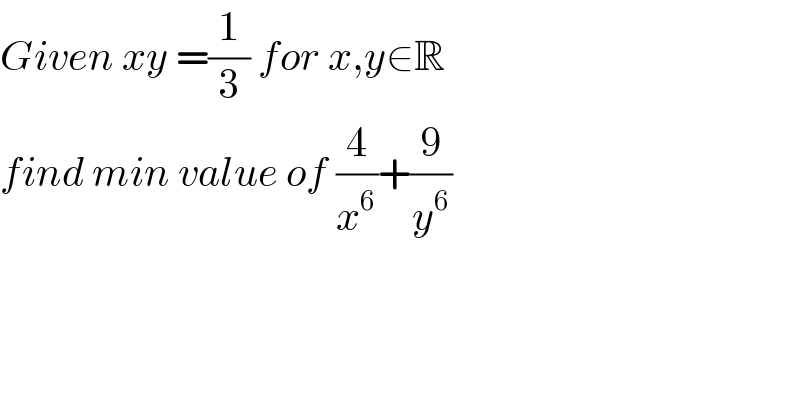
Answered by MJS_new last updated on 28/Sep/20
![y=(1/(3x)) ⇒ (4/x^6 )+(9/y^6 )=(4/x^6 )+6561x^6 (d/dx)[(4/x^6 )+6561x^6 ]=−((24)/x^7 )+39366x^5 =0 39366x^(12) =24 x^(12) =((24)/(39366))=(4/(6561)) ⇒ x=±(2^(1/6) /3^(2/3) ) ⇒ min=324](https://www.tinkutara.com/question/Q115751.png)
$${y}=\frac{\mathrm{1}}{\mathrm{3}{x}}\:\Rightarrow\:\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\frac{\mathrm{9}}{{y}^{\mathrm{6}} }=\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\mathrm{6561}{x}^{\mathrm{6}} \\ $$$$\frac{{d}}{{dx}}\left[\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\mathrm{6561}{x}^{\mathrm{6}} \right]=−\frac{\mathrm{24}}{{x}^{\mathrm{7}} }+\mathrm{39366}{x}^{\mathrm{5}} =\mathrm{0} \\ $$$$\mathrm{39366}{x}^{\mathrm{12}} =\mathrm{24} \\ $$$${x}^{\mathrm{12}} =\frac{\mathrm{24}}{\mathrm{39366}}=\frac{\mathrm{4}}{\mathrm{6561}}\:\Rightarrow\:{x}=\pm\frac{\mathrm{2}^{\mathrm{1}/\mathrm{6}} }{\mathrm{3}^{\mathrm{2}/\mathrm{3}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{min}=\mathrm{324} \\ $$
Commented by bemath last updated on 28/Sep/20
$${thank}\:{you}\:{sir} \\ $$
Answered by Olaf last updated on 28/Sep/20
![y = (1/(3x)) (x ≠0 otherwise (4/x^6 )+(9/y^6 ) doesn′t exist) f(x) = (4/x^6 )+(9/(((1/(3x)))^6 )) = (4/x^6 )+3^8 x^6 f is a even function. I suppose x > 0. f′(x) = −((4.6)/x^7 )+6.3^8 x^5 f′(x) = 0 ⇔ (6/x^7 )(3^8 x^(12) −4) = 0 ⇔ x = ((4/3^8 ))^(1/(12)) = x_1 f′(x) < 0 in ]0,x_1 [. f′(x) > 0 in ]x_1 ,+∞[. ⇒ it′s a minimum. x^6 = (√(4/3^8 )) = (2/3^4 ) = (2/(81)) y^6 = (1/(3^6 x^6 )) = (1/3^6 ).((81)/2) = (1/(18)) f(x) = (4/(((2/(81)))))+(9/(((1/(18))))) = 2.81+2.81 = 324](https://www.tinkutara.com/question/Q115749.png)
$$ \\ $$$${y}\:=\:\frac{\mathrm{1}}{\mathrm{3}{x}} \\ $$$$\left({x}\:\neq\mathrm{0}\:\mathrm{otherwise}\:\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\frac{\mathrm{9}}{{y}^{\mathrm{6}} }\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist}\right) \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\frac{\mathrm{9}}{\left(\frac{\mathrm{1}}{\mathrm{3}{x}}\right)^{\mathrm{6}} }\:=\:\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\mathrm{3}^{\mathrm{8}} {x}^{\mathrm{6}} \\ $$$${f}\:\mathrm{is}\:\mathrm{a}\:\mathrm{even}\:\mathrm{function}. \\ $$$$\mathrm{I}\:\mathrm{suppose}\:{x}\:>\:\mathrm{0}. \\ $$$${f}'\left({x}\right)\:=\:−\frac{\mathrm{4}.\mathrm{6}}{{x}^{\mathrm{7}} }+\mathrm{6}.\mathrm{3}^{\mathrm{8}} {x}^{\mathrm{5}} \\ $$$${f}'\left({x}\right)\:=\:\mathrm{0}\:\Leftrightarrow\:\frac{\mathrm{6}}{{x}^{\mathrm{7}} }\left(\mathrm{3}^{\mathrm{8}} {x}^{\mathrm{12}} −\mathrm{4}\right)\:=\:\mathrm{0} \\ $$$$\Leftrightarrow\:{x}\:=\:\sqrt[{\mathrm{12}}]{\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{8}} }}\:=\:{x}_{\mathrm{1}} \\ $$$$\left.{f}'\left({x}\right)\:<\:\mathrm{0}\:\mathrm{in}\:\right]\mathrm{0},{x}_{\mathrm{1}} \left[.\right. \\ $$$$\left.{f}'\left({x}\right)\:>\:\mathrm{0}\:\mathrm{in}\:\right]{x}_{\mathrm{1}} ,+\infty\left[.\right. \\ $$$$\Rightarrow\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{minimum}. \\ $$$${x}^{\mathrm{6}} \:=\:\sqrt{\frac{\mathrm{4}}{\mathrm{3}^{\mathrm{8}} }}\:=\:\frac{\mathrm{2}}{\mathrm{3}^{\mathrm{4}} }\:=\:\frac{\mathrm{2}}{\mathrm{81}} \\ $$$${y}^{\mathrm{6}} \:=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} {x}^{\mathrm{6}} }\:=\:\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{6}} }.\frac{\mathrm{81}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{18}} \\ $$$${f}\left({x}\right)\:=\:\frac{\mathrm{4}}{\left(\frac{\mathrm{2}}{\mathrm{81}}\right)}+\frac{\mathrm{9}}{\left(\frac{\mathrm{1}}{\mathrm{18}}\right)}\:=\:\mathrm{2}.\mathrm{81}+\mathrm{2}.\mathrm{81}\:=\:\mathrm{324} \\ $$$$ \\ $$$$ \\ $$
Commented by bemath last updated on 28/Sep/20
$${yes}\:{sir}.\:{thank}\:{you} \\ $$
Answered by 1549442205PVT last updated on 28/Sep/20
$$\mathrm{We}\:\mathrm{have}\:\:\frac{\mathrm{4}}{{x}^{\mathrm{6}} }+\frac{\mathrm{9}}{{y}^{\mathrm{6}} }=\left(\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }−\frac{\mathrm{3}}{\mathrm{y}^{\mathrm{3}} }\right)^{\mathrm{2}} +\frac{\mathrm{12}}{\left(\mathrm{xy}\right)^{\mathrm{3}} } \\ $$$$\geqslant\frac{\mathrm{12}}{\left(\mathrm{xy}\right)^{\mathrm{3}} }=\mathrm{12}×\mathrm{3}^{\mathrm{3}} =\mathrm{324} \\ $$$$\mathrm{The}\:\mathrm{equality}\:\mathrm{ocurrs}\:\mathrm{if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if} \\ $$$$\begin{cases}{\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{3}}{\mathrm{y}^{\mathrm{3}} }}\\{\mathrm{xy}=\frac{\mathrm{1}}{\mathrm{3}}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{xy}=\mathrm{1}/\mathrm{3}}\\{\mathrm{2}×\mathrm{27y}^{\mathrm{3}} =\frac{\mathrm{3}}{\mathrm{y}^{\mathrm{3}} }}\end{cases} \\ $$$$\Leftrightarrow\begin{cases}{\mathrm{y}^{\mathrm{6}} =\mathrm{1}/\mathrm{18}}\\{\mathrm{xy}=\mathrm{1}/\mathrm{3}}\end{cases}\Leftrightarrow\begin{cases}{\mathrm{y}=\frac{\mathrm{1}}{\:\:^{\mathrm{6}} \sqrt{\mathrm{18}}}}\\{\mathrm{x}=\frac{\:^{\mathrm{6}} \sqrt{\mathrm{18}}}{\mathrm{3}}}\end{cases} \\ $$$$\mathrm{Thus},\left(\frac{\mathrm{2}}{\mathrm{x}^{\mathrm{3}} }=\frac{\mathrm{3}}{\mathrm{y}^{\mathrm{3}} }\right)_{\mathrm{min}} =\mathrm{324} \\ $$$$\mathrm{when\begin{cases}{\mathrm{y}=\frac{\mathrm{1}}{\:\:^{\mathrm{6}} \sqrt{\mathrm{18}}}}\\{\mathrm{x}=\frac{\:^{\mathrm{6}} \sqrt{\mathrm{18}}}{\mathrm{3}}}\end{cases}} \\ $$