Question Number 155983 by MathsFan last updated on 06/Oct/21

$$\:{given}\:\:{y}=\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}\:,\:{then} \\ $$$$\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}+\boldsymbol{{k}}{y}=\mathrm{0}.\:{find}\:\boldsymbol{{k}} \\ $$
Commented by cortano last updated on 06/Oct/21

$$\mathrm{k}=\mathrm{1} \\ $$
Commented by yeti123 last updated on 07/Oct/21
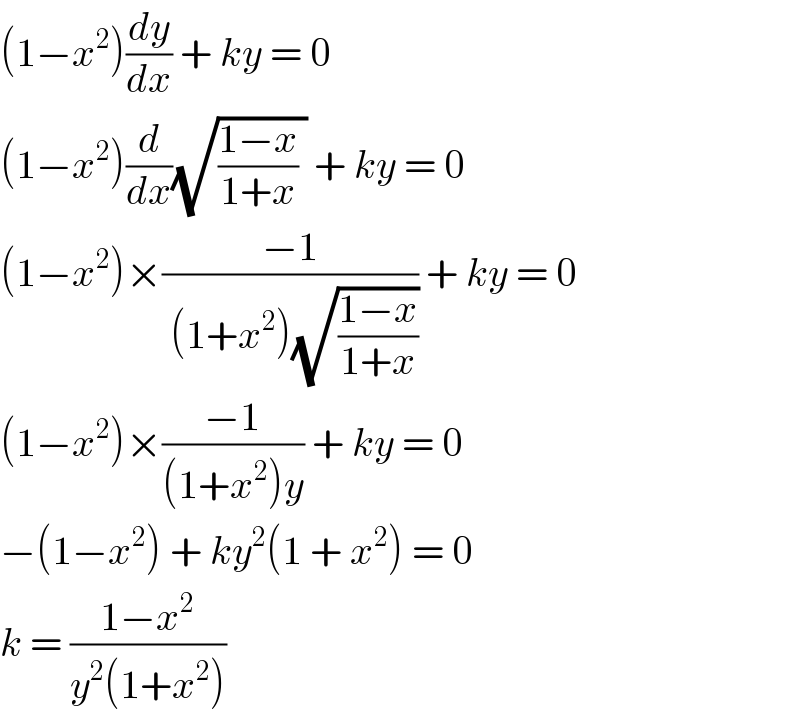
$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}\:+\:{ky}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{d}}{{dx}}\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:}\:+\:{ky}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)×\frac{−\mathrm{1}}{\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}}}\:+\:{ky}\:=\:\mathrm{0} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)×\frac{−\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}}\:+\:{ky}\:=\:\mathrm{0} \\ $$$$−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\:+\:{ky}^{\mathrm{2}} \left(\mathrm{1}\:+\:{x}^{\mathrm{2}} \right)\:=\:\mathrm{0} \\ $$$${k}\:=\:\frac{\mathrm{1}−{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\: \\ $$
Answered by puissant last updated on 06/Oct/21
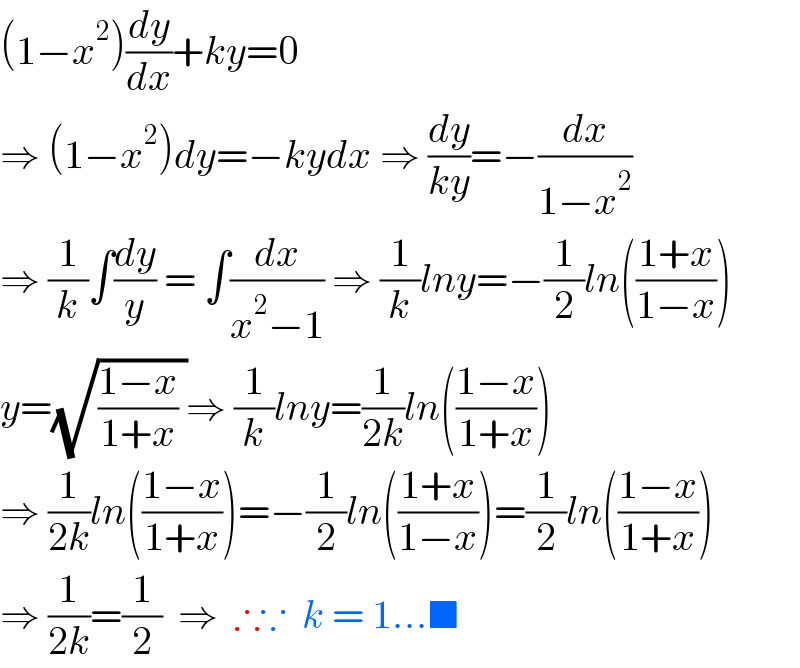
$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}+{ky}=\mathrm{0} \\ $$$$\Rightarrow\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dy}=−{kydx}\:\Rightarrow\:\frac{{dy}}{{ky}}=−\frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{k}}\int\frac{{dy}}{{y}}\:=\:\int\frac{{dx}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\Rightarrow\:\frac{\mathrm{1}}{{k}}{lny}=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right) \\ $$$${y}=\sqrt{\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\:}\Rightarrow\:\frac{\mathrm{1}}{{k}}{lny}=\frac{\mathrm{1}}{\mathrm{2}{k}}{ln}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}{k}}{ln}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)=−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right) \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}{k}}=\frac{\mathrm{1}}{\mathrm{2}}\:\:\Rightarrow\:\:\therefore\because\:\:{k}\:=\:\mathrm{1}…\blacksquare \\ $$
Commented by MathsFan last updated on 07/Oct/21

$${merci} \\ $$
Commented by puissant last updated on 07/Oct/21

$${D}'{accord}\:{j}'{espere}\:{que}\:{tous}\:{est}\:{claire}.. \\ $$
Commented by MathsFan last updated on 07/Oct/21

$${oui}\:{monsieur} \\ $$
