Question Number 170410 by Mastermind last updated on 23/May/22
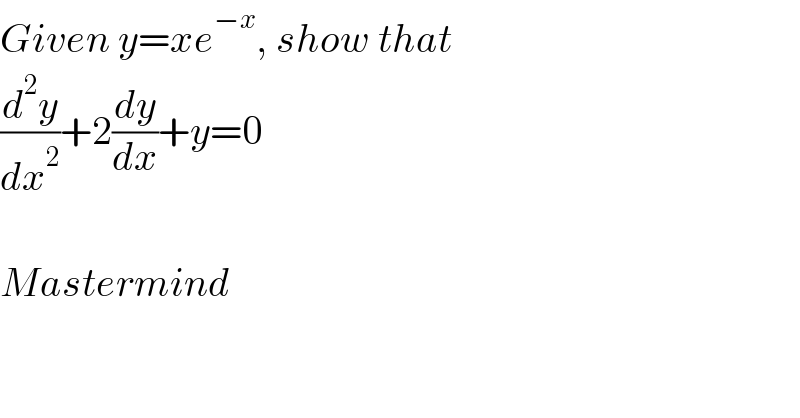
$${Given}\:{y}={xe}^{−{x}} ,\:{show}\:{that} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }+\mathrm{2}\frac{{dy}}{{dx}}+{y}=\mathrm{0} \\ $$$$ \\ $$$${Mastermind} \\ $$
Answered by floor(10²Eta[1]) last updated on 23/May/22
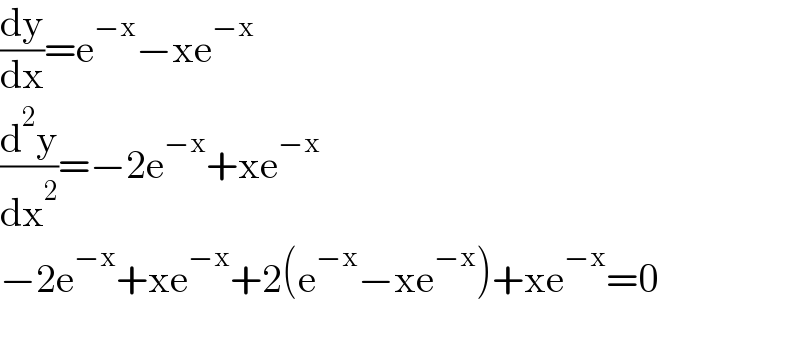
$$\frac{\mathrm{dy}}{\mathrm{dx}}=\mathrm{e}^{−\mathrm{x}} −\mathrm{xe}^{−\mathrm{x}} \\ $$$$\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }=−\mathrm{2e}^{−\mathrm{x}} +\mathrm{xe}^{−\mathrm{x}} \\ $$$$−\mathrm{2e}^{−\mathrm{x}} +\mathrm{xe}^{−\mathrm{x}} +\mathrm{2}\left(\mathrm{e}^{−\mathrm{x}} −\mathrm{xe}^{−\mathrm{x}} \right)+\mathrm{xe}^{−\mathrm{x}} =\mathrm{0} \\ $$$$ \\ $$
Commented by Mastermind last updated on 24/May/22
$${Thanks}\:{for}\:{answering}\:{my}\:{question} \\ $$
Answered by MikeH last updated on 23/May/22
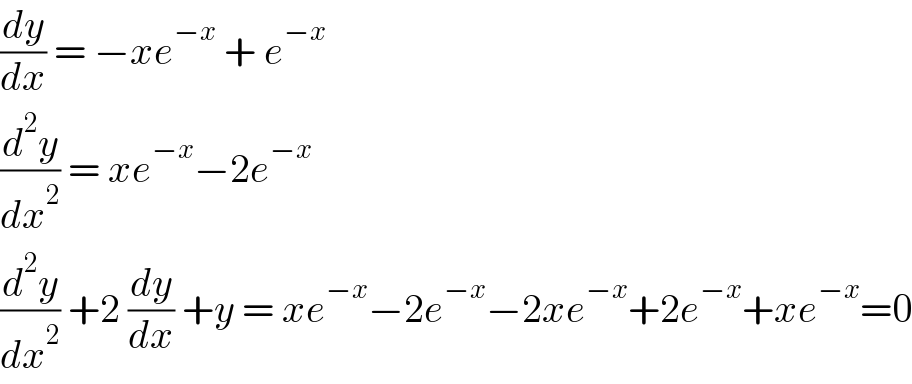
$$\frac{{dy}}{{dx}}\:=\:−{xe}^{−{x}} \:+\:{e}^{−{x}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:{xe}^{−{x}} −\mathrm{2}{e}^{−{x}} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\mathrm{2}\:\frac{{dy}}{{dx}}\:+{y}\:=\:{xe}^{−{x}} −\mathrm{2}{e}^{−{x}} −\mathrm{2}{xe}^{−{x}} +\mathrm{2}{e}^{−{x}} +{xe}^{−{x}} =\mathrm{0} \\ $$
Commented by Mastermind last updated on 24/May/22

$$ \\ $$$${Thanks}\:{man} \\ $$
