Question Number 165471 by leonhard77 last updated on 02/Feb/22
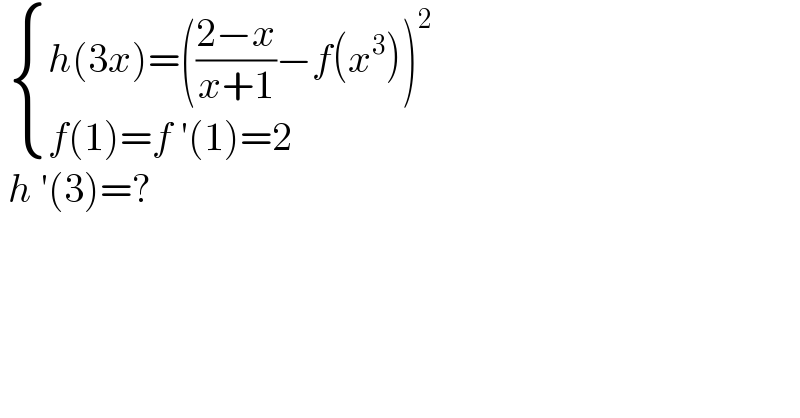
$$\:\begin{cases}{{h}\left(\mathrm{3}{x}\right)=\left(\frac{\mathrm{2}−{x}}{{x}+\mathrm{1}}−{f}\left({x}^{\mathrm{3}} \right)\right)^{\mathrm{2}} }\\{{f}\left(\mathrm{1}\right)={f}\:'\left(\mathrm{1}\right)=\mathrm{2}}\end{cases} \\ $$$$\:{h}\:'\left(\mathrm{3}\right)=? \\ $$
Commented by cortano1 last updated on 04/Feb/22
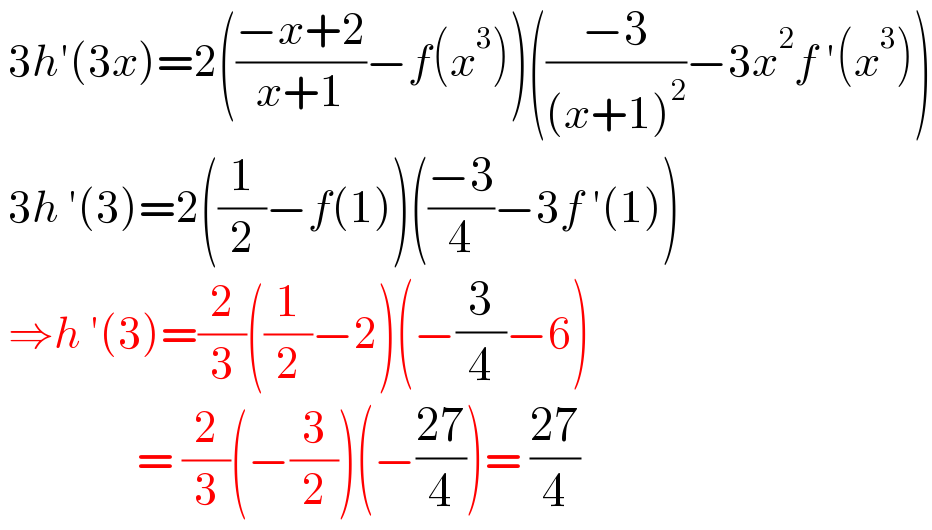
$$\:\mathrm{3}{h}'\left(\mathrm{3}{x}\right)=\mathrm{2}\left(\frac{−{x}+\mathrm{2}}{{x}+\mathrm{1}}−{f}\left({x}^{\mathrm{3}} \right)\right)\left(\frac{−\mathrm{3}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{3}{x}^{\mathrm{2}} {f}\:'\left({x}^{\mathrm{3}} \right)\right) \\ $$$$\:\mathrm{3}{h}\:'\left(\mathrm{3}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}−{f}\left(\mathrm{1}\right)\right)\left(\frac{−\mathrm{3}}{\mathrm{4}}−\mathrm{3}{f}\:'\left(\mathrm{1}\right)\right) \\ $$$$\:\Rightarrow{h}\:'\left(\mathrm{3}\right)=\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)\left(−\frac{\mathrm{3}}{\mathrm{4}}−\mathrm{6}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2}}{\mathrm{3}}\left(−\frac{\mathrm{3}}{\mathrm{2}}\right)\left(−\frac{\mathrm{27}}{\mathrm{4}}\right)=\:\frac{\mathrm{27}}{\mathrm{4}} \\ $$
