Question Number 154286 by EDWIN88 last updated on 16/Sep/21
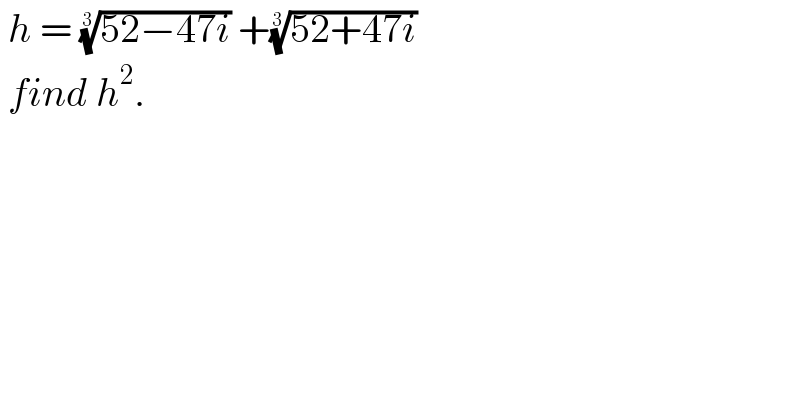
$$\:{h}\:=\:\sqrt[{\mathrm{3}}]{\mathrm{52}−\mathrm{47}{i}}\:+\sqrt[{\mathrm{3}}]{\mathrm{52}+\mathrm{47}{i}}\: \\ $$$$\:{find}\:{h}^{\mathrm{2}} . \\ $$
Commented by MJS_new last updated on 16/Sep/21
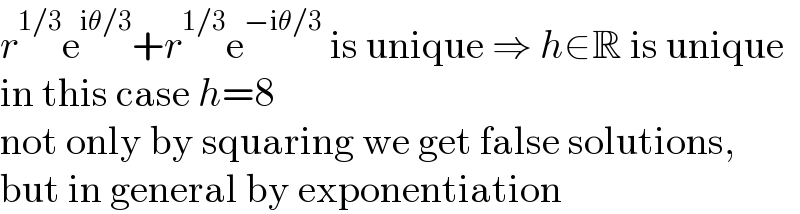
$${r}^{\mathrm{1}/\mathrm{3}} \mathrm{e}^{\mathrm{i}\theta/\mathrm{3}} +{r}^{\mathrm{1}/\mathrm{3}} \mathrm{e}^{−\mathrm{i}\theta/\mathrm{3}} \:\mathrm{is}\:\mathrm{unique}\:\Rightarrow\:{h}\in\mathbb{R}\:\mathrm{is}\:\mathrm{unique} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{h}=\mathrm{8} \\ $$$$\mathrm{not}\:\mathrm{only}\:\mathrm{by}\:\mathrm{squaring}\:\mathrm{we}\:\mathrm{get}\:\mathrm{false}\:\mathrm{solutions}, \\ $$$$\mathrm{but}\:\mathrm{in}\:\mathrm{general}\:\mathrm{by}\:\mathrm{exponentiation} \\ $$
Commented by liberty last updated on 17/Sep/21
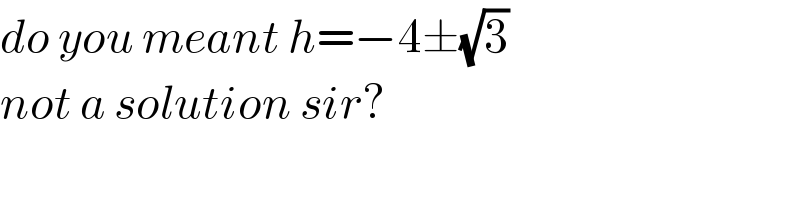
$${do}\:{you}\:{meant}\:{h}=−\mathrm{4}\pm\sqrt{\mathrm{3}} \\ $$$${not}\:{a}\:{solution}\:{sir}? \\ $$
Commented by MJS_new last updated on 17/Sep/21

$$\mathrm{yes} \\ $$
Commented by liberty last updated on 17/Sep/21
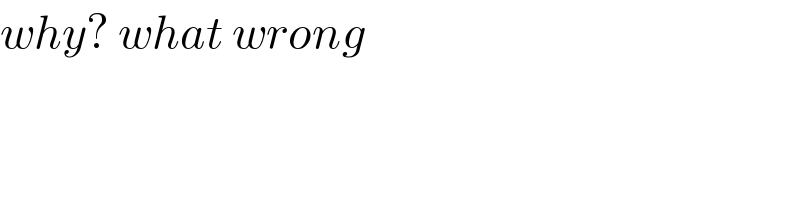
$${why}?\:{what}\:{wrong} \\ $$
Commented by MJS_new last updated on 17/Sep/21

$$\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{solve}\:\mathrm{anything}\:\mathrm{when}\:\mathrm{we}\:\mathrm{calculate} \\ $$$$\mathrm{a}\:\mathrm{root}.\:\sqrt{\mathrm{4}}=\mathrm{2}.\:\sqrt[{\mathrm{3}}]{\mathrm{8}}=\mathrm{2}.\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{a}\:\mathrm{calculation}. \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{different}\:\mathrm{if}\:\mathrm{we}\:\mathrm{solve}\:\mathrm{an}\:\mathrm{equation} \\ $$$${x}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow\:{x}=\pm\mathrm{2} \\ $$$${x}^{\mathrm{3}} =\mathrm{8}\:\Rightarrow\:{x}=\mathrm{2}\vee{x}=−\mathrm{1}\pm\mathrm{i}\sqrt{\mathrm{3}} \\ $$$$\mathrm{because}\:\mathrm{here}\:\mathrm{we}\:\mathrm{search}\:\mathrm{for}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{values} \\ $$$$\mathrm{of}\:{x}\:\mathrm{satisfying}\:{x}^{\mathrm{2}} =\mathrm{4}\:\mathrm{or}\:{x}^{\mathrm{3}} =\mathrm{8} \\ $$$$ \\ $$$${h}=\sqrt{\mathrm{25}}+\sqrt{\mathrm{9}}\:\mathrm{is}\:\mathrm{unique}:\:{h}=\mathrm{8} \\ $$$$\mathrm{you}\:\mathrm{would}\:\mathrm{not}\:\mathrm{do}\:\mathrm{this}: \\ $$$${h}=\pm\mathrm{5}\pm\mathrm{3}\:\Rightarrow\:{h}=−\mathrm{8}\vee{h}=−\mathrm{2}\vee{h}=\mathrm{2}\vee{h}=\mathrm{8} \\ $$$$\mathrm{now} \\ $$$${h}=\sqrt[{\mathrm{3}}]{\mathrm{52}−\mathrm{47i}}+\sqrt[{\mathrm{3}}]{\mathrm{52}+\mathrm{47i}} \\ $$$$\mathrm{abs}\:\left(\mathrm{52}\pm\mathrm{47i}\right)\:=\mathrm{17}\sqrt{\mathrm{17}}\:\approx\mathrm{70}.\mathrm{0928} \\ $$$$\mathrm{arg}\:\left(\mathrm{52}−\mathrm{47i}\right)\:=−\mathrm{arctan}\:\frac{\mathrm{47}}{\mathrm{52}}\:\approx−\mathrm{42}.\mathrm{1087}° \\ $$$$\mathrm{arg}\:\left(\mathrm{52}+\mathrm{47i}\right)\:=\mathrm{arctan}\:\frac{\mathrm{47}}{\mathrm{52}}\:\approx\mathrm{42}.\mathrm{1087}° \\ $$$$\mathrm{abs}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{52}\pm\mathrm{47i}}\right)\:=\sqrt[{\mathrm{3}}]{\mathrm{abs}\:\left(\mathrm{52}\pm\mathrm{47i}\right)}\:=\sqrt{\mathrm{17}} \\ $$$$\mathrm{arg}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{52}−\mathrm{47i}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arg}\:\left(\mathrm{52}−\mathrm{47i}\right)\:=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{47}}{\mathrm{52}}\:\approx−\mathrm{14}.\mathrm{0362}° \\ $$$$\mathrm{arg}\:\left(\sqrt[{\mathrm{3}}]{\mathrm{52}+\mathrm{47i}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arg}\:\left(\mathrm{52}+\mathrm{47i}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{47}}{\mathrm{52}}\:\approx\mathrm{14}.\mathrm{0362}° \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{52}−\mathrm{47i}}=\mathrm{4}−\mathrm{i} \\ $$$$\sqrt[{\mathrm{3}}]{\mathrm{52}+\mathrm{47i}}=\mathrm{4}+\mathrm{i} \\ $$$${h}=\mathrm{8} \\ $$
Answered by liberty last updated on 16/Sep/21
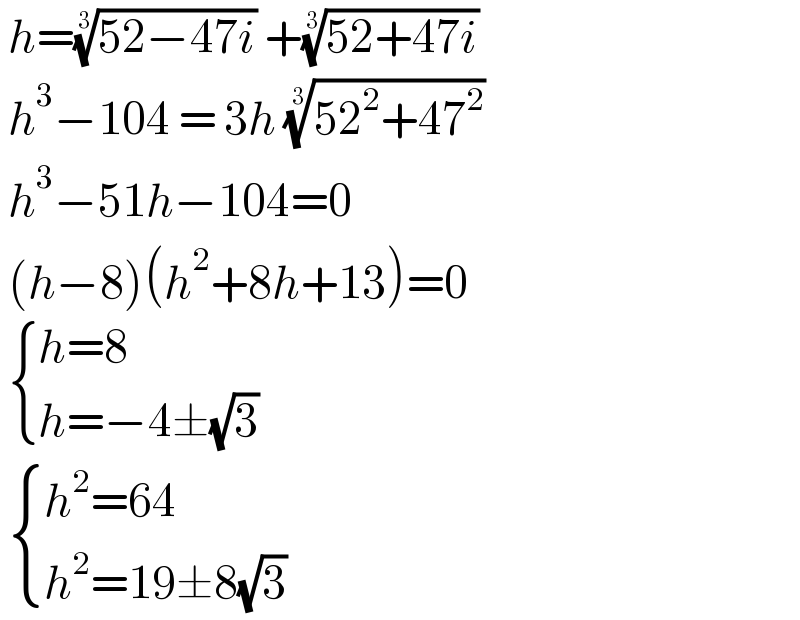
$$\:{h}=\sqrt[{\mathrm{3}}]{\mathrm{52}−\mathrm{47}{i}}\:+\sqrt[{\mathrm{3}}]{\mathrm{52}+\mathrm{47}{i}} \\ $$$$\:{h}^{\mathrm{3}} −\mathrm{104}\:=\:\mathrm{3}{h}\:\sqrt[{\mathrm{3}}]{\mathrm{52}^{\mathrm{2}} +\mathrm{47}^{\mathrm{2}} } \\ $$$$\:{h}^{\mathrm{3}} −\mathrm{51}{h}−\mathrm{104}=\mathrm{0} \\ $$$$\:\left({h}−\mathrm{8}\right)\left({h}^{\mathrm{2}} +\mathrm{8}{h}+\mathrm{13}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{{h}=\mathrm{8}}\\{{h}=−\mathrm{4}\pm\sqrt{\mathrm{3}}\:}\end{cases} \\ $$$$\:\begin{cases}{{h}^{\mathrm{2}} =\mathrm{64}}\\{{h}^{\mathrm{2}} =\mathrm{19}\pm\mathrm{8}\sqrt{\mathrm{3}}}\end{cases} \\ $$
