Question Number 16133 by Tinkutara last updated on 18/Jun/17

$$\mathrm{H}_{\alpha} \:\mathrm{line}\:\mathrm{of}\:\mathrm{Balmer}\:\mathrm{series}\:\mathrm{is}\:\mathrm{6500}\:\overset{\mathrm{o}} {\mathrm{A}}.\:\mathrm{The} \\ $$$$\mathrm{wave}\:\mathrm{length}\:\mathrm{of}\:\mathrm{H}\gamma\:\mathrm{is} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{4815}\:\overset{\mathrm{o}} {\mathrm{A}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{4298}\:\overset{\mathrm{o}} {\mathrm{A}} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{7800}\:\overset{\mathrm{o}} {\mathrm{A}} \\ $$$$\left(\mathrm{4}\right)\:\mathrm{3800}\:\overset{\mathrm{o}} {\mathrm{A}} \\ $$
Answered by ajfour last updated on 18/Jun/17
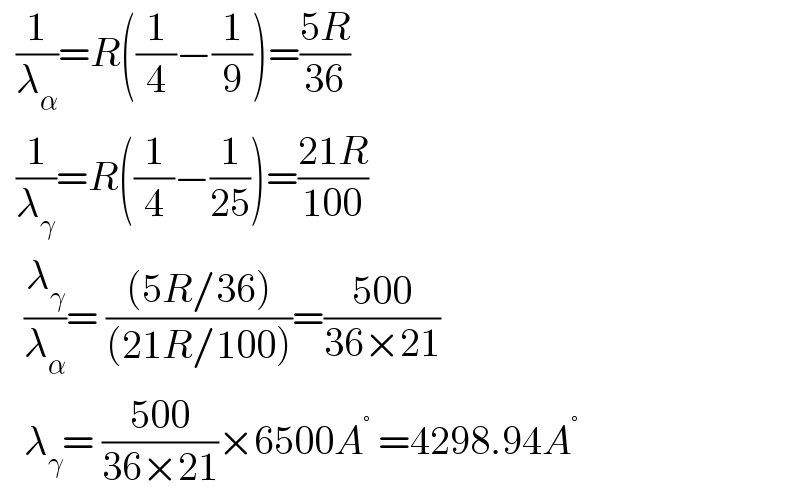
$$\:\:\frac{\mathrm{1}}{\lambda_{\alpha} }={R}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{9}}\right)=\frac{\mathrm{5}{R}}{\mathrm{36}} \\ $$$$\:\:\frac{\mathrm{1}}{\lambda_{\gamma} }={R}\left(\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{25}}\right)=\frac{\mathrm{21}{R}}{\mathrm{100}} \\ $$$$\:\:\:\frac{\lambda_{\gamma} }{\lambda_{\alpha} }=\:\frac{\left(\mathrm{5}{R}/\mathrm{36}\right)}{\left(\mathrm{21}{R}/\mathrm{100}\right)}=\frac{\mathrm{500}}{\mathrm{36}×\mathrm{21}} \\ $$$$\:\:\:\lambda_{\gamma} =\:\frac{\mathrm{500}}{\mathrm{36}×\mathrm{21}}×\mathrm{6500}{A}^{°} \:=\mathrm{4298}.\mathrm{94}{A}^{°} \\ $$
Commented by Tinkutara last updated on 18/Jun/17
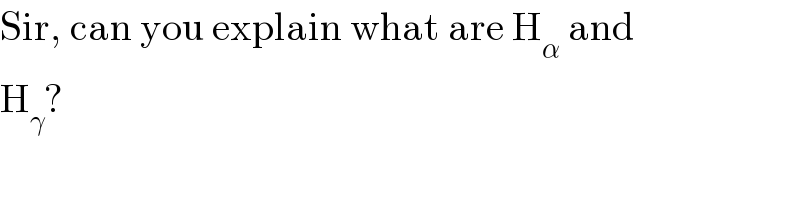
$$\mathrm{Sir},\:\mathrm{can}\:\mathrm{you}\:\mathrm{explain}\:\mathrm{what}\:\mathrm{are}\:\mathrm{H}_{\alpha} \:\mathrm{and} \\ $$$$\mathrm{H}_{\gamma} ? \\ $$
Commented by ajfour last updated on 18/Jun/17
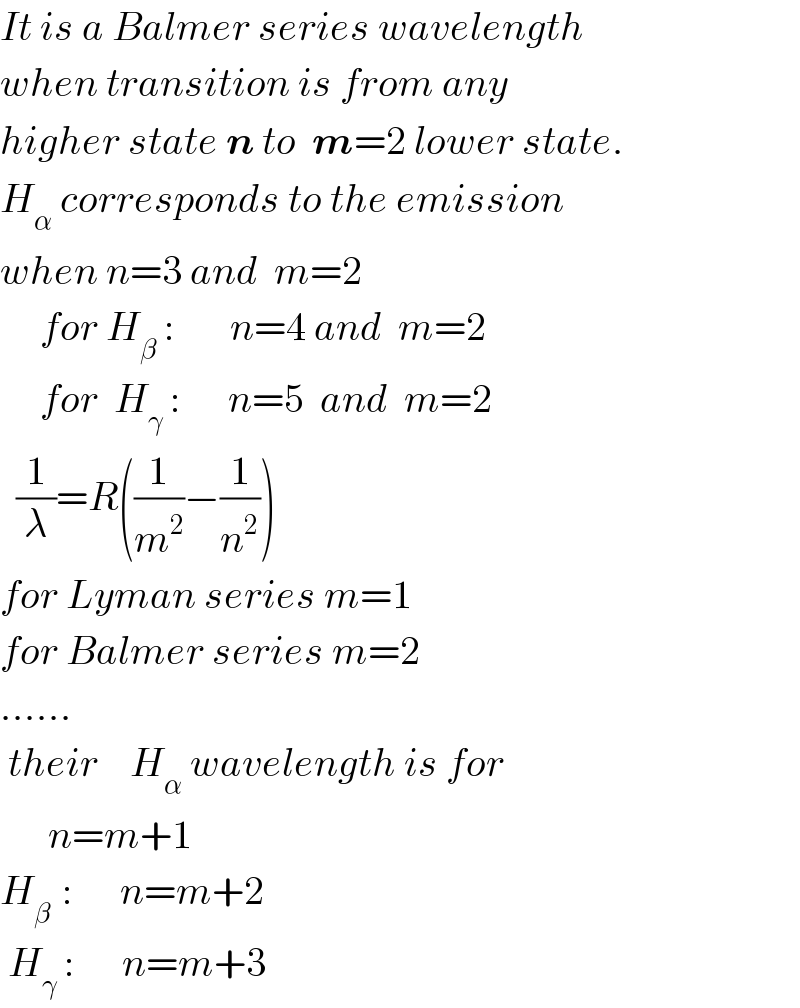
$${It}\:{is}\:{a}\:{Balmer}\:{series}\:{wavelength} \\ $$$${when}\:{transition}\:{is}\:{from}\:{any} \\ $$$${higher}\:{state}\:\boldsymbol{{n}}\:{to}\:\:\boldsymbol{{m}}=\mathrm{2}\:{lower}\:{state}. \\ $$$${H}_{\alpha} \:{corresponds}\:{to}\:{the}\:{emission} \\ $$$${when}\:{n}=\mathrm{3}\:{and}\:\:{m}=\mathrm{2} \\ $$$$\:\:\:\:\:{for}\:{H}_{\beta} \::\:\:\:\:\:\:\:{n}=\mathrm{4}\:{and}\:\:{m}=\mathrm{2}\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:{for}\:\:{H}_{\gamma} \::\:\:\:\:\:\:{n}=\mathrm{5}\:\:{and}\:\:{m}=\mathrm{2} \\ $$$$\:\:\frac{\mathrm{1}}{\lambda}={R}\left(\frac{\mathrm{1}}{{m}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right) \\ $$$${for}\:{Lyman}\:{series}\:{m}=\mathrm{1} \\ $$$${for}\:{Balmer}\:{series}\:{m}=\mathrm{2} \\ $$$$…… \\ $$$$\:{their}\:\:\:\:{H}_{\alpha} \:{wavelength}\:{is}\:{for}\: \\ $$$$\:\:\:\:\:\:{n}={m}+\mathrm{1} \\ $$$${H}_{\beta\:} \::\:\:\:\:\:\:{n}={m}+\mathrm{2} \\ $$$$\:{H}_{\gamma} \::\:\:\:\:\:\:{n}={m}+\mathrm{3} \\ $$
Commented by Tinkutara last updated on 18/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
