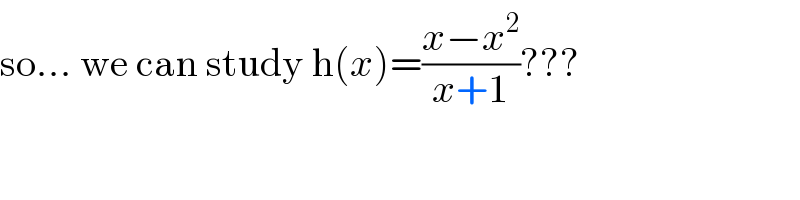Question Number 80180 by mathocean1 last updated on 31/Jan/20

Answered by Rio Michael last updated on 31/Jan/20

Commented by mathocean1 last updated on 31/Jan/20
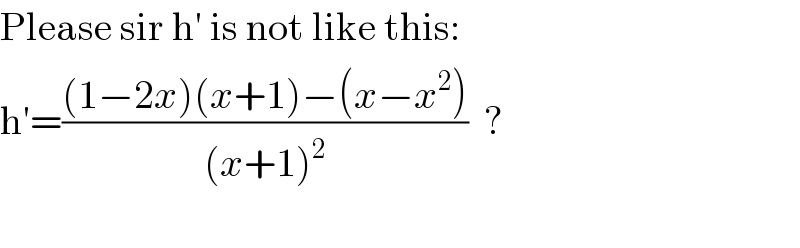
Commented by mathocean1 last updated on 31/Jan/20

Commented by Rio Michael last updated on 31/Jan/20
Commented by mathocean1 last updated on 31/Jan/20

Commented by JDamian last updated on 01/Feb/20
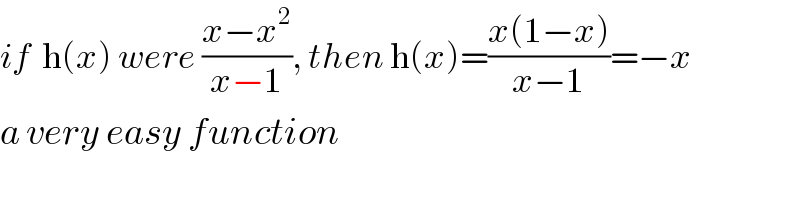
Commented by mathocean1 last updated on 01/Feb/20