Question Number 100829 by M±th+et+s last updated on 28/Jun/20
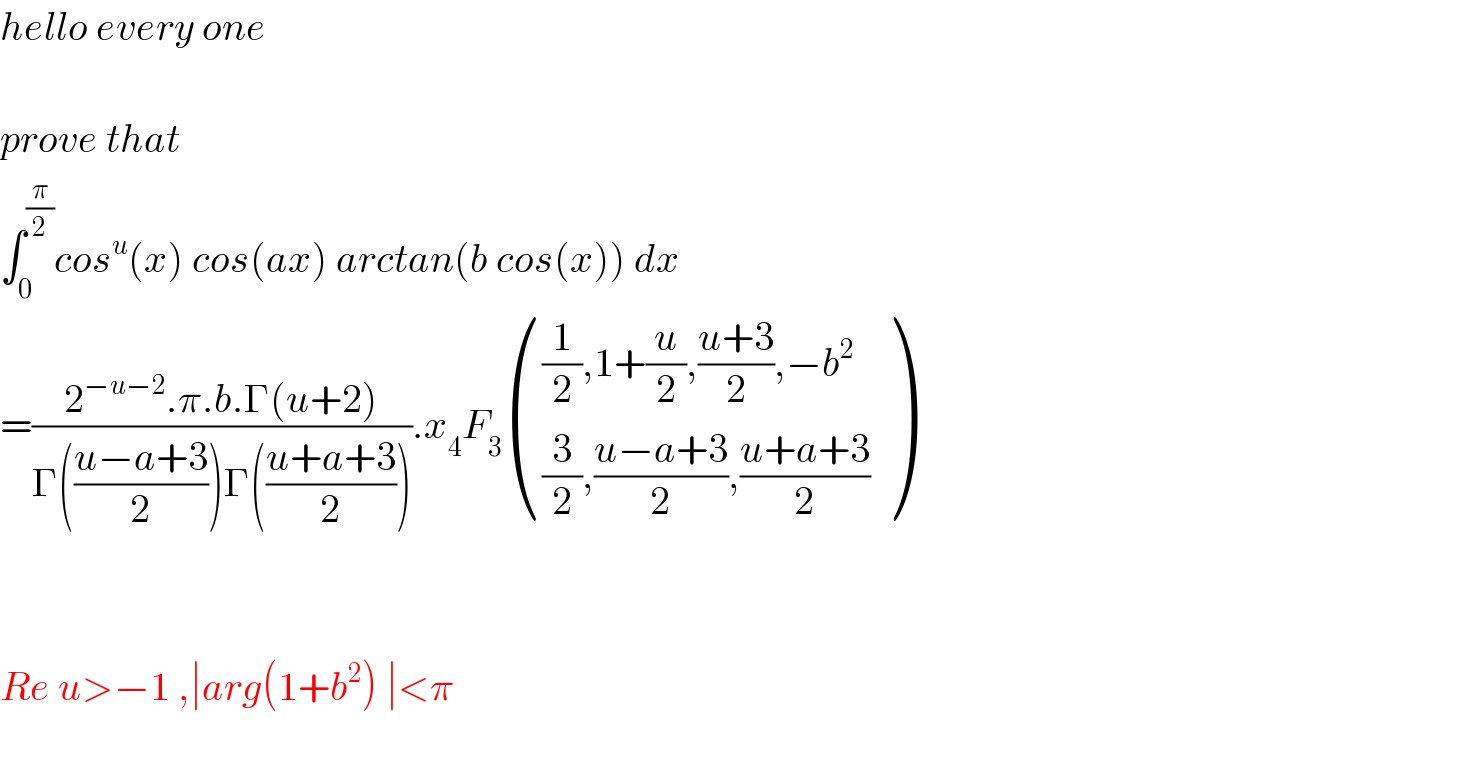
$${hello}\:{every}\:{one}\: \\ $$$$ \\ $$$${prove}\:{that} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{{u}} \left({x}\right)\:{cos}\left({ax}\right)\:{arctan}\left({b}\:{cos}\left({x}\right)\right)\:{dx} \\ $$$$=\frac{\mathrm{2}^{−{u}−\mathrm{2}} .\pi.{b}.\Gamma\left({u}+\mathrm{2}\right)}{\Gamma\left(\frac{{u}−{a}+\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{{u}+{a}+\mathrm{3}}{\mathrm{2}}\right)}.{x}_{\mathrm{4}} {F}_{\mathrm{3}} \begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}},\mathrm{1}+\frac{{u}}{\mathrm{2}},\frac{{u}+\mathrm{3}}{\mathrm{2}},−{b}^{\mathrm{2}} }\\{\frac{\mathrm{3}}{\mathrm{2}},\frac{{u}−{a}+\mathrm{3}}{\mathrm{2}},\frac{{u}+{a}+\mathrm{3}}{\mathrm{2}}}\end{pmatrix} \\ $$$$ \\ $$$$ \\ $$$${Re}\:{u}>−\mathrm{1}\:,\mid{arg}\left(\mathrm{1}+{b}^{\mathrm{2}} \right)\:\mid<\pi \\ $$$$ \\ $$
