Question Number 97271 by M±th+et+s last updated on 07/Jun/20
$${hello}\:{every}\:{one} \\ $$$${why}\:{do}\:{planets}\:{of}\:{the}\:{solar}\:{system} \\ $$$${revolve}\:{around}\:{the}\:{sun}\:{in}\:{an}\:{eliptical} \\ $$$${not}\:{circular}\:{orbit} \\ $$
Commented by mr W last updated on 07/Jun/20
$${if}\:{we}\:{had}\:{a}\:{two}−{body}\:{system}\: \\ $$$${consisting}\:{of}\:{the}\:{sun}\:{and}\:{a}\:{planet} \\ $$$${and}\:{the}\:{only}\:{force}\:{acting}\:{between}\: \\ $$$${them}\:{is}\:{the}\:{gravitational}\:{force}\:{and} \\ $$$${both}\:{objects}\:{are}\:{seen}\:{as}\:{point}\:{masses}, \\ $$$${it}\:{can}\:{be}\:{proved}\:{that}\:{the}\:{orbit}\:{of}\:{the} \\ $$$${planet}\:{around}\:{the}\:{sun}\:{is}\:{an}\:{ellipse}. \\ $$$${the}\:{shape}\:{of}\:{the}\:{ellipse}\:{depents}\:{on} \\ $$$${the}\:{initial}\:{condition}.\:{in}\:{special} \\ $$$${condition},\:{the}\:{orbit}\:{can}\:{be}\:{a}\:{circle} \\ $$$${which}\:{is}\:{also}\:{a}\:{special}\:{form}\:{of}\:{ellipse}. \\ $$$${but}\:{the}\:{real}\:{solar}\:{system}\:{is}\:{much}\:{more} \\ $$$${complicated}\:{than}\:{a}\:{two}−{body}\:{system}, \\ $$$${there}\:{are}\:{several}\:{planets}\:{which} \\ $$$${affect}\:{each}\:{other}\:{and}\:{both}\:{the}\:{sun} \\ $$$${and}\:{the}\:{planets}\:{are}\:{not}\:{point}\:{masses}, \\ $$$${therefore}\:{the}\:{real}\:{orbits}\:{of}\:{the}\:{planets} \\ $$$${are}\:{not}\:{perfect}\:{ellipses},\:{only}\:{near} \\ $$$${ellipses}.\:{a}\:{circular}\:{orbit}\:{is}\:{too}\:{perfect}, \\ $$$${which}\:{can}\:{not}\:{be}\:{kept}\:{stable}\:{in}\:{nature}, \\ $$$${because}\:{any}\:{disturbance}\:{may}\:{let}\:{it} \\ $$$${leave}\:{this}\:{perfect}\:{form}.\:{nevertheless} \\ $$$${the}\:{orbit}\:{of}\:{Venus}\:{is}\:{almost}\:{a}\:{circle}. \\ $$
Commented by M±th+et+s last updated on 08/Jun/20
$${thank}\:{you}\:{sir} \\ $$
Answered by Sourav mridha last updated on 07/Jun/20
![okk let′s see the trajectory of body moving in central force field...but Here i am not using GTR..only the point of view of old classical concept of Newtonian Lagrangian Mechanics. let′s pick up the example of our solar system....where sun is at the focus and earth moves round sun in account of Gravitational force feild. so our Lagrangian constracted in plane polar coordinate like that L=(1/2)[(r^• )^2 +r^2 (𝛉^• )^2 ]−v(r) now using Euler−Lagrange eq^n (from Variational calculas) (∂L/∂r)−(d/dt)((∂L/∂r^• ))=0 and (∂L/∂𝛉)−(d/dt)((∂L/∂𝛉^• ))=0 from 1st eq^n we get r^(••) −r(𝛉^• )^2 =−(∂/∂r)[v(r)]=F(r)=(k/r^2 ) .................(i) F(r)=gravitetional force ,k=constant k=Gm_s m_e . and 2nd eq^n gives us r^2 𝛉^• =constant,multi:𝛍 both sides we get L=𝛍r^2 𝛉=constant ...........(ii) where 𝛍=((m_s m_e )/(m_s +m_e ))=reduce mass for central force− torque 𝛕 =r^→ ×f(r)=0 or (dL/dt)=constant where L=angular momentam. now let u=(1/r) now diff wrt to 𝛉 and using eq^n (ii) we get (du/d𝛉)=((−1)/r^2 ).((dr/dt)/(d𝛉/dt))=−(1/r^2 )(r^• /𝛉^• )=−(𝛍/L)r^• now (d^2 u/d𝛉^2 )=−(𝛍^2 /(L^2 u^2 )).r^(••) . so we get r^(••) =−((L^2 u^2 )/𝛍^2 ).(d^2 u/d𝛉^2 ) and r(𝛉^• )^2 =((u^3 L^2 )/𝛍^2 )... now putting this two results at eq^n (i) we get eq^(n ) of motion of earth around sun is (d^2 u/d𝛉^2 )+u=−((𝛍^2 k)/L^2 )(constant) by solving this easy 2nd ODE we get u(𝛉)=−((𝛍^2 k)/L^2 )+Acos𝛉+Bsin𝛉 or =−((𝛍^2 k)/L^2 )+𝛄cos𝚽 we considerate at first u=(1/r) so now r(𝚽)=(1/(−((𝛍^2 k)/L^2 )+γcos(𝚽))) =((−(L^2 /(𝛍^2 k)))/(1−((L^2 𝛄)/(μ^2 k))cos(𝚽))) compare this result with eq^n of a ellipse in plane polar coordinate r(𝛉)=(l/(1+_− ecos(𝛉))) in our case−− sami letus rectum of the ellipticak path of our planet is l=a(1−e^2 )=−(L^2 /(𝛍^2 k)) and escentricity e=((L^2 𝛄)/(𝛍^2 k)) this is why planets arw moving in a elliptical path... 1st proposed by Kepler in his 1st las of planetory motion..](https://www.tinkutara.com/question/Q97384.png)
$$\boldsymbol{{okk}}\:\boldsymbol{{let}}'\boldsymbol{{s}}\:\boldsymbol{{see}}\:\boldsymbol{{the}}\:\boldsymbol{{trajectory}}\:\boldsymbol{{of}} \\ $$$$\boldsymbol{{body}}\:\boldsymbol{{moving}}\:\boldsymbol{{in}}\:\boldsymbol{{central}}\:\boldsymbol{{force}}\: \\ $$$$\boldsymbol{{field}}…\boldsymbol{{but}}\:\boldsymbol{{H}}\mathrm{ere}\:\boldsymbol{{i}}\:\boldsymbol{{am}}\:\boldsymbol{{not}}\:\boldsymbol{{using}} \\ $$$$\boldsymbol{{GTR}}..\mathrm{only}\:\boldsymbol{{the}}\:\boldsymbol{{point}}\:\boldsymbol{{of}}\:\boldsymbol{{view}}\:\boldsymbol{{of}} \\ $$$$\boldsymbol{{old}}\:\boldsymbol{{classical}}\:\boldsymbol{{concept}}\:\boldsymbol{{of}}\:\boldsymbol{{Newtonian}} \\ $$$$\boldsymbol{{Lagrangian}}\:\boldsymbol{{M}}\mathrm{e}\boldsymbol{{chanics}}. \\ $$$$\boldsymbol{{let}}'\boldsymbol{{s}}\:\boldsymbol{{pick}}\:\boldsymbol{{up}}\:\boldsymbol{{the}}\:\boldsymbol{{example}}\:\boldsymbol{{of}}\: \\ $$$$\boldsymbol{{our}}\:\boldsymbol{{solar}}\:\boldsymbol{{system}}….\boldsymbol{{where}}\:\boldsymbol{{sun}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{at}}\:\boldsymbol{{the}}\:\boldsymbol{{focus}}\:\boldsymbol{{and}}\:\boldsymbol{{earth}}\:\boldsymbol{{moves}}\: \\ $$$$\boldsymbol{{round}}\:\boldsymbol{{sun}}\:\boldsymbol{{in}}\:\boldsymbol{{account}}\:\boldsymbol{{of}}\:\boldsymbol{{Gravitational}}\:\boldsymbol{{force}}\: \\ $$$$\boldsymbol{{feild}}. \\ $$$$\:\boldsymbol{{so}}\:\boldsymbol{{our}}\:\boldsymbol{{Lagrangian}}\:\boldsymbol{{constracted}} \\ $$$$\boldsymbol{{in}}\:\boldsymbol{{plane}}\:\boldsymbol{{polar}}\:\boldsymbol{{coordinate}}\:\boldsymbol{{like}}\:\boldsymbol{{that}} \\ $$$$\:\:\:\:\:\mathscr{L}=\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\overset{\bullet} {\boldsymbol{{r}}}\right)^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{2}} \left(\overset{\bullet} {\boldsymbol{\theta}}\right)^{\mathrm{2}} \right]−\boldsymbol{{v}}\left(\boldsymbol{{r}}\right) \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{using}}\:\boldsymbol{{Euler}}−\boldsymbol{{Lagrange}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \\ $$$$\left(\boldsymbol{{from}}\:\boldsymbol{{V}}\mathrm{a}\boldsymbol{{riational}}\:\boldsymbol{{calculas}}\right) \\ $$$$\frac{\partial\mathscr{L}}{\partial\boldsymbol{{r}}}−\frac{\boldsymbol{{d}}}{\boldsymbol{{dt}}}\left(\frac{\partial\mathscr{L}}{\partial\overset{\bullet} {\boldsymbol{{r}}}}\right)=\mathrm{0}\:\boldsymbol{{and}}\:\frac{\partial\mathscr{L}}{\partial\boldsymbol{\theta}}−\frac{\boldsymbol{{d}}}{\boldsymbol{{dt}}}\left(\frac{\partial\mathscr{L}}{\partial\overset{\bullet} {\boldsymbol{\theta}}}\right)=\mathrm{0} \\ $$$$\boldsymbol{{from}}\:\mathrm{1}\boldsymbol{{st}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\boldsymbol{{we}}\:\boldsymbol{{g}}\mathrm{et} \\ $$$$\:\:\:\overset{\bullet\bullet} {\boldsymbol{{r}}}−\boldsymbol{{r}}\left(\overset{\bullet} {\boldsymbol{\theta}}\right)^{\mathrm{2}} =−\frac{\partial}{\partial\boldsymbol{{r}}}\left[\boldsymbol{{v}}\left(\boldsymbol{{r}}\right)\right]=\boldsymbol{{F}}\left(\mathrm{r}\right)=\frac{\boldsymbol{{k}}}{\boldsymbol{{r}}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……………..\left(\boldsymbol{{i}}\right) \\ $$$$\boldsymbol{{F}}\left(\mathrm{r}\right)=\boldsymbol{{gravitetional}}\:\boldsymbol{{force}}\:,\boldsymbol{{k}}=\boldsymbol{{constant}} \\ $$$$\boldsymbol{{k}}=\boldsymbol{{Gm}}_{\boldsymbol{{s}}} \boldsymbol{{m}}_{\boldsymbol{{e}}} . \\ $$$$\:\boldsymbol{{and}}\:\mathrm{2}\boldsymbol{{nd}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\boldsymbol{{gives}}\:\boldsymbol{{us}} \\ $$$$\boldsymbol{{r}}^{\mathrm{2}} \overset{\bullet} {\boldsymbol{\theta}}=\boldsymbol{{constant}},\boldsymbol{{multi}}:\boldsymbol{\mu}\:\boldsymbol{{both}}\:\boldsymbol{{sides}} \\ $$$$\boldsymbol{{we}}\:\boldsymbol{{get}}\:\boldsymbol{{L}}=\boldsymbol{\mu{r}}^{\mathrm{2}} \boldsymbol{\theta}=\boldsymbol{{constant}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:………..\left(\boldsymbol{{ii}}\right) \\ $$$$\boldsymbol{{where}}\:\boldsymbol{\mu}=\frac{\boldsymbol{{m}}_{\boldsymbol{{s}}} \boldsymbol{{m}}_{\boldsymbol{{e}}} }{\boldsymbol{{m}}_{\boldsymbol{{s}}} +\boldsymbol{{m}}_{\boldsymbol{{e}}} }=\boldsymbol{{reduce}}\:\boldsymbol{{mass}} \\ $$$$\boldsymbol{{for}}\:\boldsymbol{{central}}\:\boldsymbol{{force}}− \\ $$$$\boldsymbol{{torque}}\:\boldsymbol{\tau}\:=\overset{\rightarrow} {\boldsymbol{{r}}}×\boldsymbol{{f}}\left(\boldsymbol{{r}}\right)=\mathrm{0}\:\boldsymbol{{or}}\:\frac{\boldsymbol{{dL}}}{\boldsymbol{{dt}}}=\boldsymbol{{constant}} \\ $$$$\boldsymbol{{where}}\:\boldsymbol{{L}}=\boldsymbol{{angular}}\:\boldsymbol{{momentam}}. \\ $$$$\:\:\boldsymbol{{now}}\:\boldsymbol{{let}}\:\boldsymbol{{u}}=\frac{\mathrm{1}}{\boldsymbol{{r}}}\:\boldsymbol{{now}}\:\boldsymbol{{diff}}\:\boldsymbol{{wrt}}\:\boldsymbol{{to}}\: \\ $$$$\boldsymbol{\theta}\:\boldsymbol{{and}}\:\boldsymbol{{using}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\:\left(\boldsymbol{{ii}}\right)\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\frac{\boldsymbol{{du}}}{\boldsymbol{{d}\theta}}=\frac{−\mathrm{1}}{\boldsymbol{{r}}^{\mathrm{2}} }.\frac{\frac{\boldsymbol{{dr}}}{\boldsymbol{{dt}}}}{\frac{\boldsymbol{{d}\theta}}{\boldsymbol{{dt}}}}=−\frac{\mathrm{1}}{\boldsymbol{{r}}^{\mathrm{2}} }\frac{\overset{\bullet} {\boldsymbol{{r}}}}{\overset{\bullet} {\boldsymbol{\theta}}}=−\frac{\boldsymbol{\mu}}{\boldsymbol{{L}}}\overset{\bullet} {\boldsymbol{{r}}} \\ $$$$\boldsymbol{{now}}\:\frac{\boldsymbol{{d}}^{\mathrm{2}} \boldsymbol{{u}}}{\boldsymbol{{d}\theta}^{\mathrm{2}} }=−\frac{\boldsymbol{\mu}^{\mathrm{2}} }{\boldsymbol{{L}}^{\mathrm{2}} \boldsymbol{{u}}^{\mathrm{2}} }.\overset{\bullet\bullet} {\boldsymbol{{r}}}\:\:. \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{we}}\:\boldsymbol{{get}}\:\overset{\bullet\bullet} {\boldsymbol{{r}}}=−\frac{\boldsymbol{{L}}^{\mathrm{2}} \boldsymbol{{u}}^{\mathrm{2}} }{\boldsymbol{\mu}^{\mathrm{2}} }.\frac{\boldsymbol{{d}}^{\mathrm{2}} \boldsymbol{{u}}}{\boldsymbol{{d}\theta}^{\mathrm{2}} }\:\boldsymbol{{and}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{r}}\left(\overset{\bullet} {\boldsymbol{\theta}}\right)^{\mathrm{2}} =\frac{\boldsymbol{{u}}^{\mathrm{3}} \boldsymbol{{L}}^{\mathrm{2}} }{\boldsymbol{\mu}^{\mathrm{2}} }… \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{putting}}\:\boldsymbol{{this}}\:\boldsymbol{{two}}\:\boldsymbol{{results}}\:\boldsymbol{{at}} \\ $$$$\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\:\left(\boldsymbol{{i}}\right)\:\boldsymbol{{we}}\:\boldsymbol{{get}}\:\boldsymbol{{eq}}^{\boldsymbol{{n}}\:} \boldsymbol{{of}}\:\boldsymbol{{motion}}\:\boldsymbol{{of}}\: \\ $$$$\boldsymbol{{earth}}\:\boldsymbol{{around}}\:\boldsymbol{{sun}}\:\boldsymbol{{is}} \\ $$$$\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\boldsymbol{{d}}^{\mathrm{2}} \boldsymbol{{u}}}{\boldsymbol{{d}\theta}^{\mathrm{2}} }+\boldsymbol{{u}}=−\frac{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}}{\boldsymbol{{L}}^{\mathrm{2}} }\left(\boldsymbol{{constant}}\right) \\ $$$$\boldsymbol{{by}}\:\boldsymbol{{solving}}\:\boldsymbol{{this}}\:\boldsymbol{{easy}}\:\mathrm{2}\boldsymbol{{nd}}\:\boldsymbol{{ODE}} \\ $$$$\:\:\boldsymbol{{we}}\:\boldsymbol{{get}}\:\boldsymbol{{u}}\left(\boldsymbol{\theta}\right)=−\frac{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}}{\boldsymbol{{L}}^{\mathrm{2}} }+\boldsymbol{{Acos}\theta}+\boldsymbol{{Bsin}\theta} \\ $$$$\:\:\:\:\:\:\:\mathrm{or}\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}}{\boldsymbol{{L}}^{\mathrm{2}} }+\boldsymbol{\gamma{cos}\Phi} \\ $$$$\:\boldsymbol{{we}}\:\boldsymbol{{considerate}}\:\boldsymbol{{at}}\:\boldsymbol{{first}}\:\boldsymbol{{u}}=\frac{\mathrm{1}}{\boldsymbol{{r}}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{now}}\:\boldsymbol{{r}}\left(\boldsymbol{\Phi}\right)=\frac{\mathrm{1}}{−\frac{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}}{\boldsymbol{{L}}^{\mathrm{2}} }+\gamma\boldsymbol{{cos}}\left(\boldsymbol{\Phi}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{−\frac{\boldsymbol{{L}}^{\mathrm{2}} }{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}}}{\mathrm{1}−\frac{\boldsymbol{{L}}^{\mathrm{2}} \boldsymbol{\gamma}}{\mu^{\mathrm{2}} \boldsymbol{{k}}}\boldsymbol{{cos}}\left(\boldsymbol{\Phi}\right)} \\ $$$$\boldsymbol{{compare}}\:\boldsymbol{{this}}\:\boldsymbol{{result}}\:\boldsymbol{{with}}\: \\ $$$$\boldsymbol{{eq}}^{\boldsymbol{{n}}} \:\boldsymbol{{of}}\:\boldsymbol{{a}}\:\boldsymbol{{ellipse}}\:\boldsymbol{{in}}\:\boldsymbol{{plane}}\:\boldsymbol{{polar}} \\ $$$$\boldsymbol{{coordinate}}\:\boldsymbol{{r}}\left(\boldsymbol{\theta}\right)=\frac{\boldsymbol{{l}}}{\mathrm{1}\underset{−} {+}\boldsymbol{{ecos}}\left(\boldsymbol{\theta}\right)} \\ $$$$\boldsymbol{{in}}\:\boldsymbol{{our}}\:\boldsymbol{{case}}−− \\ $$$$\boldsymbol{{sami}}\:\boldsymbol{{letus}}\:\boldsymbol{{rectum}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{ellipticak}} \\ $$$$\boldsymbol{{path}}\:\boldsymbol{{of}}\:\boldsymbol{{our}}\:\boldsymbol{{planet}}\:\boldsymbol{{is}} \\ $$$$\boldsymbol{{l}}=\boldsymbol{{a}}\left(\mathrm{1}−\boldsymbol{{e}}^{\mathrm{2}} \right)=−\frac{\boldsymbol{{L}}^{\mathrm{2}} }{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}} \\ $$$$\boldsymbol{{and}}\:\boldsymbol{{escentricity}}\:\boldsymbol{{e}}=\frac{\boldsymbol{{L}}^{\mathrm{2}} \boldsymbol{\gamma}}{\boldsymbol{\mu}^{\mathrm{2}} \boldsymbol{{k}}} \\ $$$$\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{why}}\:\boldsymbol{{planets}}\:\boldsymbol{{arw}}\:\boldsymbol{{moving}} \\ $$$$\boldsymbol{{in}}\:\boldsymbol{{a}}\:\boldsymbol{{elliptical}}\:\boldsymbol{{path}}… \\ $$$$\mathrm{1}\boldsymbol{{st}}\:\boldsymbol{{proposed}}\:\boldsymbol{{by}}\:\boldsymbol{{K}}\mathrm{e}\boldsymbol{{pler}}\:\boldsymbol{{in}}\:\boldsymbol{{his}} \\ $$$$\mathrm{1}\boldsymbol{{st}}\:\boldsymbol{{las}}\:\boldsymbol{{of}}\:\boldsymbol{{planetory}}\:\boldsymbol{{motion}}.. \\ $$$$ \\ $$
Commented by smridha last updated on 08/Jun/20
$$\boldsymbol{{ohh}}\:\boldsymbol{{sorry}}\:\boldsymbol{{it}}\:\boldsymbol{{should}}\:\boldsymbol{{be}}\:\frac{\boldsymbol{{dL}}}{{d}\boldsymbol{{t}}}=\mathrm{0} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{L}}=\boldsymbol{{constant}}. \\ $$
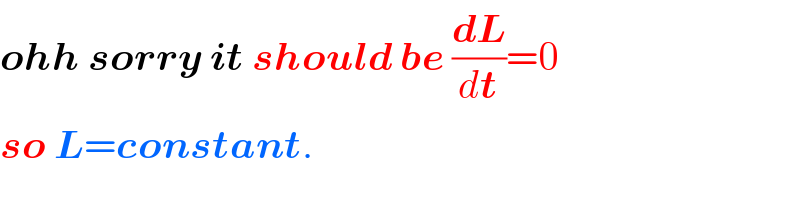
Commented by M±th+et+s last updated on 08/Jun/20
$${great}\:{work}\:{thanks} \\ $$