Menu Close

hello-please-give-me-the-limited-development-of-f-in-0-at-3-rd-order-f-x-ln-sin-x-

Tinku Tara 0 Comments
Pin




Question Number 130303 by stelor last updated on 24/Jan/21
hello... please give me the limited development of...f... in 0 at 3^(rd) order. f(x)=ln(sin(x))
$$\mathrm{hello}…\:\mathrm{please}\:\mathrm{give}\:\mathrm{me}\:\mathrm{the}\:\mathrm{limited}\:\mathrm{development}\:\mathrm{of}…{f}…\:{in}\:\mathrm{0}\:{at}\:\mathrm{3}^{{rd}} \:{order}. \\ $$$$\:\:\:\:{f}\left({x}\right)={ln}\left({sin}\left({x}\right)\right) \\ $$$$ \\ $$
Commented by stelor last updated on 24/Jan/21
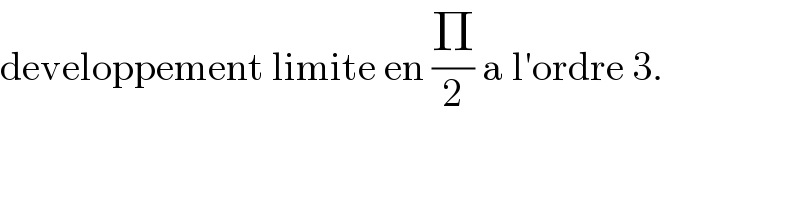
developpement limite en (Π/2) a l′ordre 3.
$$\mathrm{developpement}\:\mathrm{limite}\:\mathrm{en}\:\frac{\Pi}{\mathrm{2}}\:\mathrm{a}\:\mathrm{l}'\mathrm{ordre}\:\mathrm{3}. \\ $$
Answered by mathmax by abdo last updated on 24/Jan/21
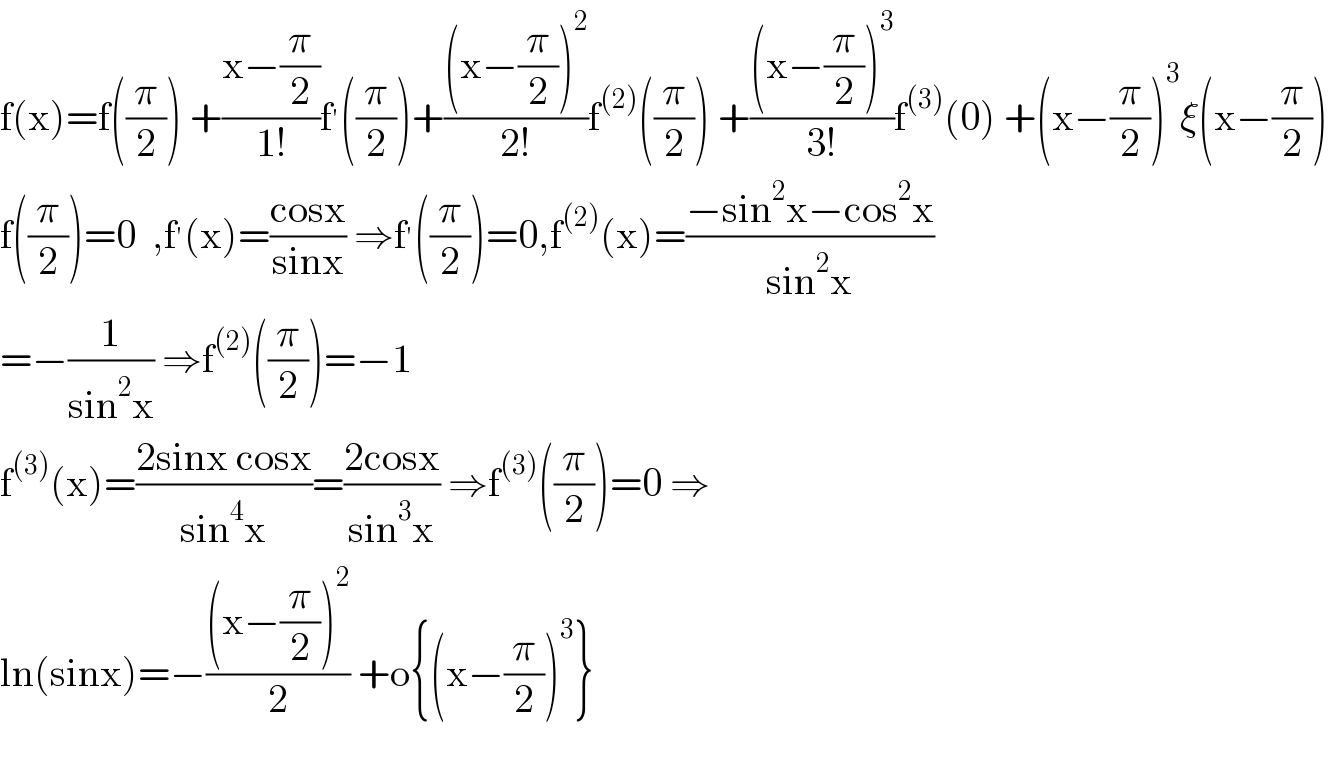
f(x)=f((π/2)) +((x−(π/2))/(1!))f^′ ((π/2))+(((x−(π/2))^2 )/(2!))f^((2)) ((π/2)) +(((x−(π/2))^3 )/(3!))f^((3)) (0) +(x−(π/2))^3 ξ(x−(π/2)) f((π/2))=0 ,f^′ (x)=((cosx)/(sinx)) ⇒f^′ ((π/2))=0,f^((2)) (x)=((−sin^2 x−cos^2 x)/(sin^2 x)) =−(1/(sin^2 x)) ⇒f^((2)) ((π/2))=−1 f^((3)) (x)=((2sinx cosx)/(sin^4 x))=((2cosx)/(sin^3 x)) ⇒f^((3)) ((π/2))=0 ⇒ ln(sinx)=−(((x−(π/2))^2 )/2) +o{(x−(π/2))^3 }
$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\frac{\pi}{\mathrm{2}}\right)\:+\frac{\mathrm{x}−\frac{\pi}{\mathrm{2}}}{\mathrm{1}!}\mathrm{f}^{'} \left(\frac{\pi}{\mathrm{2}}\right)+\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}!}\mathrm{f}^{\left(\mathrm{2}\right)} \left(\frac{\pi}{\mathrm{2}}\right)\:+\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{3}} }{\mathrm{3}!}\mathrm{f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)\:+\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{3}} \xi\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right) \\ $$$$\mathrm{f}\left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{0}\:\:,\mathrm{f}^{'} \left(\mathrm{x}\right)=\frac{\mathrm{cosx}}{\mathrm{sinx}}\:\Rightarrow\mathrm{f}^{'} \left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{0},\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right)=\frac{−\mathrm{sin}^{\mathrm{2}} \mathrm{x}−\mathrm{cos}^{\mathrm{2}} \mathrm{x}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\:\Rightarrow\mathrm{f}^{\left(\mathrm{2}\right)} \left(\frac{\pi}{\mathrm{2}}\right)=−\mathrm{1} \\ $$$$\mathrm{f}^{\left(\mathrm{3}\right)} \left(\mathrm{x}\right)=\frac{\mathrm{2sinx}\:\mathrm{cosx}}{\mathrm{sin}^{\mathrm{4}} \mathrm{x}}=\frac{\mathrm{2cosx}}{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}\:\Rightarrow\mathrm{f}^{\left(\mathrm{3}\right)} \left(\frac{\pi}{\mathrm{2}}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{sinx}\right)=−\frac{\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{2}}\:+\mathrm{o}\left\{\left(\mathrm{x}−\frac{\pi}{\mathrm{2}}\right)^{\mathrm{3}} \right\} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 24/Jan/21
first line f^((3)) ((π/2))
$$\mathrm{first}\:\mathrm{line}\:\mathrm{f}^{\left(\mathrm{3}\right)} \left(\frac{\pi}{\mathrm{2}}\right) \\ $$
Commented by stelor last updated on 25/Jan/21
merci........(√(√(thank)))
$$\mathrm{merci}……..\sqrt{\sqrt{\mathrm{thank}}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *