Question Number 166177 by RB95 last updated on 14/Feb/22

$$ \\ $$help me please
A cone 9 cm high and 8 cm in base diameter is filled with ice.
a) vanilla for 2/5 of the height,
b) chocolate for the remaining part
1. Calculate the volume of ice it contains.
2. Calculate the volume of the vanilla ice cream and the volume of the chocolate. By what fractions must the total volume of ice be multiplied to obtain these two volumes? The different volumes will be rounded to the nearest cm³.
Answered by mr W last updated on 14/Feb/22
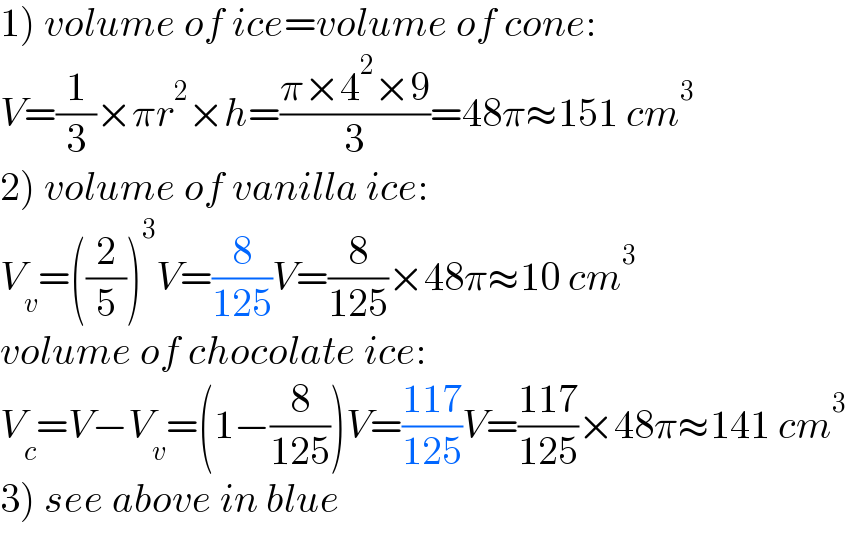
$$\left.\mathrm{1}\right)\:{volume}\:{of}\:{ice}={volume}\:{of}\:{cone}: \\ $$$${V}=\frac{\mathrm{1}}{\mathrm{3}}×\pi{r}^{\mathrm{2}} ×{h}=\frac{\pi×\mathrm{4}^{\mathrm{2}} ×\mathrm{9}}{\mathrm{3}}=\mathrm{48}\pi\approx\mathrm{151}\:{cm}^{\mathrm{3}} \\ $$$$\left.\mathrm{2}\right)\:{volume}\:{of}\:{vanilla}\:{ice}: \\ $$$${V}_{{v}} =\left(\frac{\mathrm{2}}{\mathrm{5}}\right)^{\mathrm{3}} {V}=\frac{\mathrm{8}}{\mathrm{125}}{V}=\frac{\mathrm{8}}{\mathrm{125}}×\mathrm{48}\pi\approx\mathrm{10}\:{cm}^{\mathrm{3}} \\ $$$${volume}\:{of}\:{chocolate}\:{ice}: \\ $$$${V}_{{c}} ={V}−{V}_{{v}} =\left(\mathrm{1}−\frac{\mathrm{8}}{\mathrm{125}}\right){V}=\frac{\mathrm{117}}{\mathrm{125}}{V}=\frac{\mathrm{117}}{\mathrm{125}}×\mathrm{48}\pi\approx\mathrm{141}\:{cm}^{\mathrm{3}} \\ $$$$\left.\mathrm{3}\right)\:{see}\:{above}\:{in}\:{blue} \\ $$
Commented by Tawa11 last updated on 16/Feb/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$
