Question Number 182438 by neinhaltsieger369 last updated on 09/Dec/22
![[Help me!] The rate of change of w = x^3 y^2 z + y^3 z^2 − xz^4 at the point Q(0, 1, 2) in the direction V^→ = 2i + j + 2k is: a) −2 b) −3 c) −4 d) No alternative](https://www.tinkutara.com/question/Q182438.png)
$$\: \\ $$$$\:\left[\boldsymbol{\mathrm{Help}}\:\:\boldsymbol{\mathrm{me}}!\right] \\ $$$$\: \\ $$$$\:\boldsymbol{\mathrm{The}}\:\:\boldsymbol{\mathrm{rate}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{change}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{w}}\:\:=\:\:\boldsymbol{\mathrm{x}}^{\mathrm{3}} \boldsymbol{\mathrm{y}}^{\mathrm{2}} \boldsymbol{\mathrm{z}}\:\:+\:\boldsymbol{\mathrm{y}}^{\mathrm{3}} \boldsymbol{\mathrm{z}}^{\mathrm{2}} \:−\:\boldsymbol{\mathrm{xz}}^{\mathrm{4}} \:\:\boldsymbol{\mathrm{at}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{point}}\:\:\boldsymbol{\mathrm{Q}}\left(\mathrm{0},\:\mathrm{1},\:\mathrm{2}\right) \\ $$$$\:\boldsymbol{\mathrm{in}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{direction}}\:\:\overset{\rightarrow} {\boldsymbol{\mathrm{V}}}\:\:=\:\:\mathrm{2}\boldsymbol{\mathrm{i}}\:\:+\:\:\boldsymbol{\mathrm{j}}\:\:+\:\:\mathrm{2}\boldsymbol{\mathrm{k}}\:\:\boldsymbol{\mathrm{is}}: \\ $$$$\: \\ $$$$\left.\:\boldsymbol{\mathrm{a}}\right)\:−\mathrm{2} \\ $$$$\left.\:\boldsymbol{\mathrm{b}}\right)\:−\mathrm{3} \\ $$$$\left.\:\boldsymbol{\mathrm{c}}\right)\:−\mathrm{4} \\ $$$$\left.\:\boldsymbol{\mathrm{d}}\right)\:\boldsymbol{\mathrm{No}}\:\:\boldsymbol{\mathrm{alternative}} \\ $$$$\: \\ $$
Answered by mr W last updated on 09/Dec/22
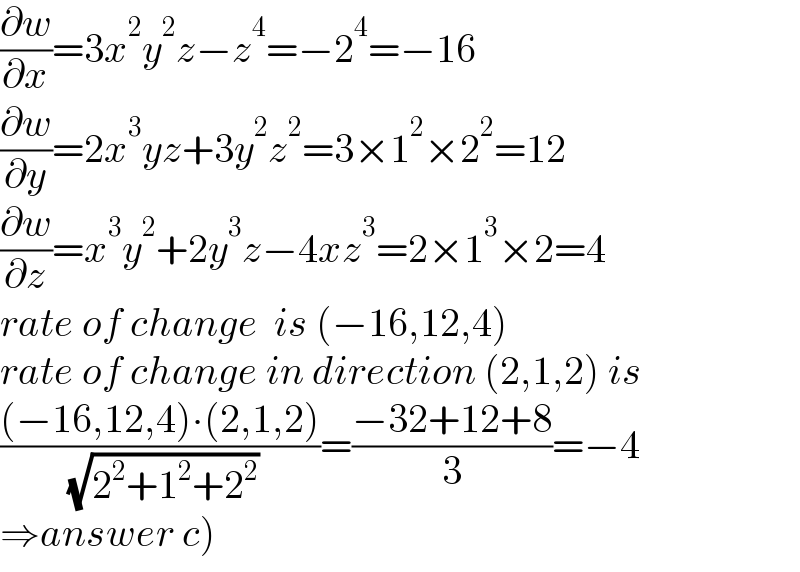
$$\frac{\partial{w}}{\partial{x}}=\mathrm{3}{x}^{\mathrm{2}} {y}^{\mathrm{2}} {z}−{z}^{\mathrm{4}} =−\mathrm{2}^{\mathrm{4}} =−\mathrm{16} \\ $$$$\frac{\partial{w}}{\partial{y}}=\mathrm{2}{x}^{\mathrm{3}} {yz}+\mathrm{3}{y}^{\mathrm{2}} {z}^{\mathrm{2}} =\mathrm{3}×\mathrm{1}^{\mathrm{2}} ×\mathrm{2}^{\mathrm{2}} =\mathrm{12} \\ $$$$\frac{\partial{w}}{\partial{z}}={x}^{\mathrm{3}} {y}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{3}} {z}−\mathrm{4}{xz}^{\mathrm{3}} =\mathrm{2}×\mathrm{1}^{\mathrm{3}} ×\mathrm{2}=\mathrm{4} \\ $$$${rate}\:{of}\:{change}\:\:{is}\:\left(−\mathrm{16},\mathrm{12},\mathrm{4}\right) \\ $$$${rate}\:{of}\:{change}\:{in}\:{direction}\:\left(\mathrm{2},\mathrm{1},\mathrm{2}\right)\:{is} \\ $$$$\frac{\left(−\mathrm{16},\mathrm{12},\mathrm{4}\right)\centerdot\left(\mathrm{2},\mathrm{1},\mathrm{2}\right)}{\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} }}=\frac{−\mathrm{32}+\mathrm{12}+\mathrm{8}}{\mathrm{3}}=−\mathrm{4} \\ $$$$\left.\Rightarrow{answer}\:{c}\right) \\ $$
Commented by neinhaltsieger369 last updated on 09/Dec/22

$$\: \\ $$$$\:{Thank}\:\:{you}! \\ $$$$\: \\ $$$$\:{I}\:\:{understood} \\ $$$$\: \\ $$$$:-\mathrm{D} \\ $$
