Question Number 90301 by zainal tanjung last updated on 22/Apr/20
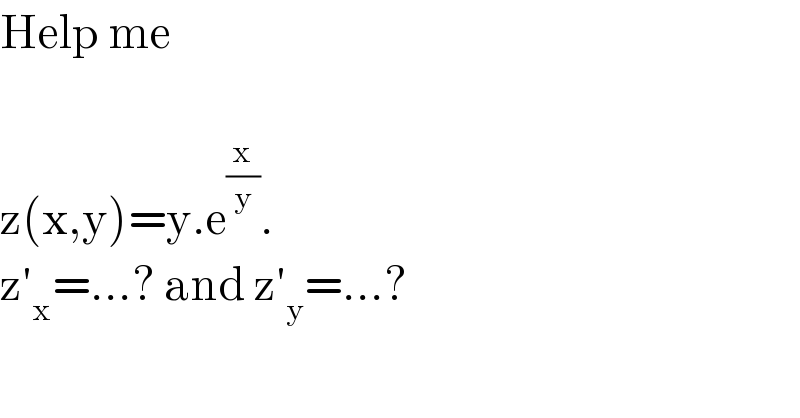
$$\mathrm{Help}\:\mathrm{me} \\ $$$$ \\ $$$$\mathrm{z}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{y}.\mathrm{e}^{\frac{\mathrm{x}}{\mathrm{y}}} . \\ $$$$\mathrm{z}'_{\mathrm{x}} =…?\:\mathrm{and}\:\mathrm{z}'_{\mathrm{y}} =…? \\ $$
Commented by mathmax by abdo last updated on 23/Apr/20

$${z}\left({x},{y}\right)\:={y}\:{e}^{\frac{{x}}{{y}}} \:\Rightarrow\frac{\partial{z}}{\partial{x}}\left({x},{y}\right)\:=\frac{\mathrm{1}}{{y}}{y}\:{e}^{\frac{{x}}{{y}}} \:={e}^{\frac{{x}}{{y}}} \\ $$$$\frac{\partial{z}}{\partial{y}}\left({x},{y}\right)\:={e}^{\frac{{x}}{{y}}} \:+{y}\left(−\frac{{x}}{{y}^{\mathrm{2}} }{e}^{\frac{{x}}{{y}}} \right)\:={e}^{\frac{{x}}{{y}}} −\frac{{x}}{{y}}{e}^{\frac{{x}}{{y}}} \:=\left(\mathrm{1}−\frac{{x}}{{y}}\right){e}^{\frac{{x}}{{y}}} \\ $$
