Question Number 41707 by Necxx last updated on 11/Aug/18
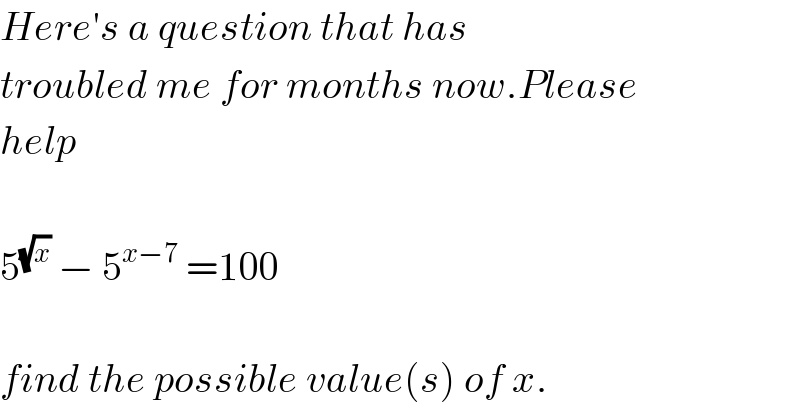
$${Here}'{s}\:{a}\:{question}\:{that}\:{has} \\ $$$${troubled}\:{me}\:{for}\:{months}\:{now}.{Please} \\ $$$${help} \\ $$$$ \\ $$$$\mathrm{5}^{\sqrt{{x}}} \:−\:\mathrm{5}^{{x}−\mathrm{7}} \:=\mathrm{100} \\ $$$$ \\ $$$${find}\:{the}\:{possible}\:{value}\left({s}\right)\:{of}\:{x}. \\ $$
Answered by alex041103 last updated on 11/Aug/18

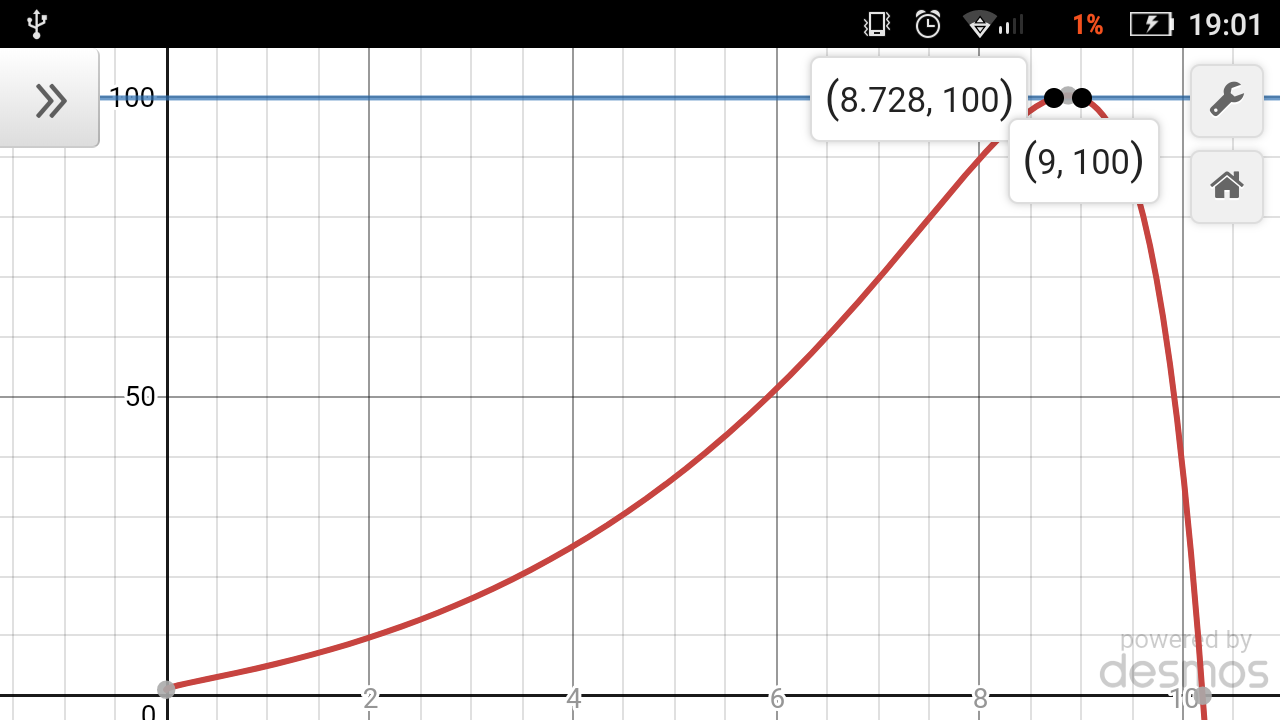
$${let}\:{f}\left({x}\right)=\mathrm{5}^{\sqrt{{x}}} −\mathrm{5}^{{x}−\mathrm{7}} \\ $$$${We}\:{wantf}\left({x}\right)>\mathrm{0} \\ $$$$\Rightarrow\mathrm{5}^{\sqrt{{x}}} >\mathrm{5}^{{x}−\mathrm{7}} \\ $$$$\Rightarrow\sqrt{{x}}>{x}−\mathrm{7} \\ $$$${let}\:{u}=\sqrt{{x}},\:{u}>\mathrm{0} \\ $$$$\Rightarrow{u}^{\mathrm{2}} −{u}−\mathrm{7}<\mathrm{0} \\ $$$$\:{for}\:{u}\in\left(\frac{\mathrm{1}−\sqrt{\mathrm{29}}}{\mathrm{2}},\:\frac{\mathrm{1}+\sqrt{\mathrm{29}}}{\mathrm{2}}\right)\cup\left(\mathrm{0},\infty\right) \\ $$$$\Rightarrow\sqrt{{x}}\in\left(\mathrm{0},\:\frac{\mathrm{1}+\sqrt{\mathrm{29}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{x}\in\left(\mathrm{0},\frac{\mathrm{15}+\sqrt{\mathrm{29}}}{\mathrm{2}}\right)\approx\left(\mathrm{0},\:\mathrm{10}.\mathrm{19}\right) \\ $$$$\Rightarrow{solutions}\:{will}\:{be}\:{between}\:\mathrm{0}\:{and}\:\mathrm{10}.\mathrm{19} \\ $$$${We}\:{can}\:{immediatly}\:{see}\:{that} \\ $$$${x}=\mathrm{9}\:{is}\:{a}\:{solution}. \\ $$$${We}\:{see}\:{that}\:{f}\:'\left({x}\right)={ln}\left(\mathrm{5}\right)\left(\frac{\mathrm{5}^{\sqrt{{x}}} }{\mathrm{2}\sqrt{{x}}}−\mathrm{5}^{{x}−\mathrm{7}} \right). \\ $$$${We}\:{see}\:{that}\:{f}\:'\left(\mathrm{9}\right)<\mathrm{0}\Rightarrow{the}\:{function} \\ $$$${has}\:{values}\:{biger}\:{than}\:\mathrm{100}. \\ $$$${By}\:{initializing}\:{numerical}\:{methods} \\ $$$${we}\:{see}\:{that}\:{x}\approx\mathrm{8}.\mathrm{73}\:{is}\:{a}\:{solution}. \\ $$$${By}\:{initializing}\:{the}\:{graph}\:{of}\:{f} \\ $$$${we}\:{see}\:{that}\:{there}\:{are}\:\mathrm{2}\:{solutions}. \\ $$$${Ans}.\:{x}=\mathrm{9}\:{and}\:{x}\approx\mathrm{8}.\mathrm{73} \\ $$
Commented by alex041103 last updated on 11/Aug/18
Commented by alex041103 last updated on 11/Aug/18
$${for}\:{example}−\:{Newton}'{s}\:{method} \\ $$
Commented by Necxx last updated on 11/Aug/18
$${which}\:{numerical}\:{method}\:{did}\:{you} \\ $$$${apply}? \\ $$
Commented by Necxx last updated on 11/Aug/18

$${thanks}\:{boss} \\ $$
Answered by peter frank last updated on 04/Oct/18
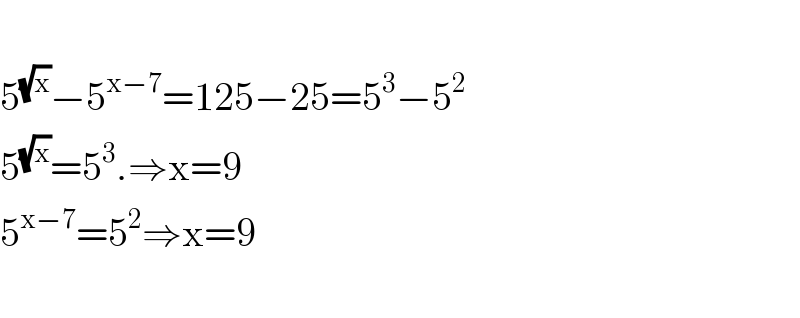
$$ \\ $$$$\mathrm{5}^{\sqrt{\mathrm{x}}} −\mathrm{5}^{\mathrm{x}−\mathrm{7}} =\mathrm{125}−\mathrm{25}=\mathrm{5}^{\mathrm{3}} −\mathrm{5}^{\mathrm{2}} \\ $$$$\mathrm{5}^{\sqrt{\mathrm{x}}} =\mathrm{5}^{\mathrm{3}} .\Rightarrow\mathrm{x}=\mathrm{9} \\ $$$$\mathrm{5}^{\mathrm{x}−\mathrm{7}} =\mathrm{5}^{\mathrm{2}} \Rightarrow\mathrm{x}=\mathrm{9} \\ $$$$ \\ $$
