Question Number 89399 by mathocean1 last updated on 17/Apr/20

$$\mathrm{Hi}. \\ $$$$\mathrm{A}\:\mathrm{ballot}\:\mathrm{box}\:\mathrm{contains}\:\mathrm{3}\:\mathrm{red}\:\mathrm{balls},\:\mathrm{4}\:\mathrm{blues} \\ $$$$\mathrm{balls}\:\mathrm{and}\:\mathrm{5}\:\mathrm{white}\:\mathrm{balls}. \\ $$$$\mathrm{we}\:\mathrm{draw}\:\mathrm{successively}\:\mathrm{3}\:\mathrm{balls}\:\mathrm{in}\:\mathrm{ballot}\:\mathrm{box}\: \\ $$$$\mathrm{by}\:\mathrm{re}−\mathrm{puting}\:\mathrm{the}\:\mathrm{drawn}\:\mathrm{balls}. \\ $$$$\left.\mathrm{1}\right)\mathrm{Calculate}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{draws}\: \\ $$$$\mathrm{containing}\:\mathrm{one}\:\mathrm{ball}\:\mathrm{of}\:\mathrm{each}\:\mathrm{color}. \\ $$
Commented by mr W last updated on 17/Apr/20

$${the}\:{question}\:{is}\:{not}\:{clear}\:{at}\:{all}\:{to}\:{me}! \\ $$$${what}\:{means}\:“{by}\:{re}−{puting}\:{the}\:{drawn} \\ $$$${balls}''\:{exactly}?\:{does}\:{it}\:{mean}\:{that}\:{every} \\ $$$${time}\:{when}\:{a}\:{ball}\:{is}\:{drawn}\:{it}\:{will}\:{be} \\ $$$${put}\:{into}\:{the}\:{box}\:{before}\:{the}\:{next}\:{draw}? \\ $$$${or}\:{it}\:{means}\:{that}\:{at}\:{first}\:{three}\:{ball}\:{are} \\ $$$${drawn}\:{and}\:{then}\:{put}\:{into}\:{the}\:{box}? \\ $$$${what}\:{means}\:“\mathrm{the}\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{draws}\:\mathrm{containing}\:\mathrm{one}\:\mathrm{ball}\:\mathrm{of}\:\mathrm{each} \\ $$$$\mathrm{color}''? \\ $$
Commented by jagoll last updated on 17/Apr/20
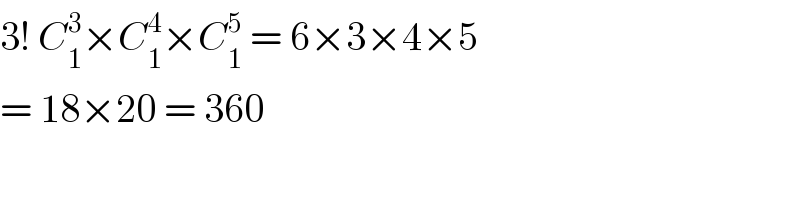
$$\mathrm{3}!\:{C}_{\mathrm{1}} ^{\mathrm{3}} ×{C}_{\mathrm{1}} ^{\mathrm{4}} ×{C}_{\mathrm{1}} ^{\mathrm{5}} \:=\:\mathrm{6}×\mathrm{3}×\mathrm{4}×\mathrm{5} \\ $$$$=\:\mathrm{18}×\mathrm{20}\:=\:\mathrm{360} \\ $$
Commented by jagoll last updated on 17/Apr/20

$${according}\:{to}\:{my}\:{understand}\: \\ $$$${taking}\:{the}\:{ball}\:{one}\:{by}\:{one}\:{with}\: \\ $$$${return}\:.\:{the}\:{second}\:{ball}\:{is}\:{taken}\: \\ $$$${after}\:{the}\:{first}\:{ball}\:{is}\:{returned}\: \\ $$$${again} \\ $$
Commented by mathocean1 last updated on 17/Apr/20
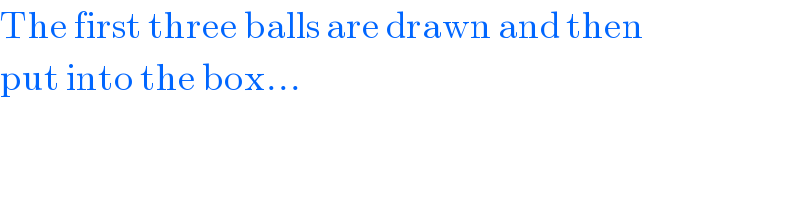
$$\mathrm{The}\:\mathrm{first}\:\mathrm{three}\:\mathrm{balls}\:\mathrm{are}\:\mathrm{drawn}\:\mathrm{and}\:\mathrm{then} \\ $$$$\mathrm{put}\:\mathrm{into}\:\mathrm{the}\:\mathrm{box}… \\ $$
Commented by mathocean1 last updated on 17/Apr/20
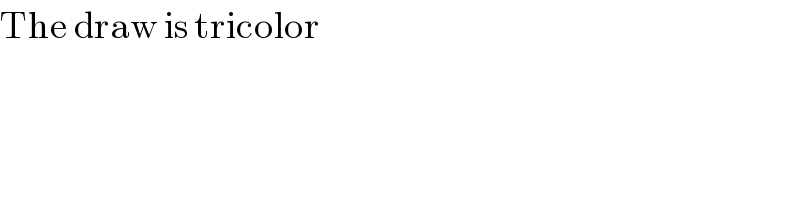
$$\mathrm{The}\:\mathrm{draw}\:\mathrm{is}\:\mathrm{tricolor} \\ $$
Commented by mr W last updated on 17/Apr/20

$${then}\:{the}\:{question}\:{should}\:{be}: \\ $$$${three}\:{balls}\:{are}\:{drawn}\:{from}\:{the}\:{box}, \\ $$$${what}\:{is}\:{the}\:{probability}\:{that}\:{one}\:{ball} \\ $$$${of}\:{each}\:{color}\:{is}\:{drawn}. \\ $$$${right}\:{sir}? \\ $$
Commented by mathocean1 last updated on 17/Apr/20
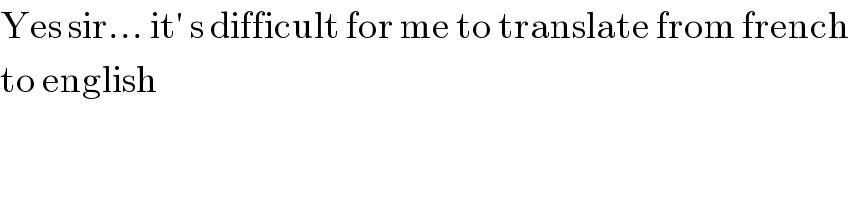
$$\mathrm{Yes}\:\mathrm{sir}…\:\mathrm{it}'\:\mathrm{s}\:\mathrm{difficult}\:\mathrm{for}\:\mathrm{me}\:\mathrm{to}\:\mathrm{translate}\:\mathrm{from}\:\mathrm{french} \\ $$$$\mathrm{to}\:\mathrm{english}\: \\ $$
Commented by mr W last updated on 17/Apr/20

$${alright}\:{sir}!\:{now}\:{we}\:{know}\:{the}\:{exact} \\ $$$${question}\:{and}\:{can}\:{solve}\:{it}. \\ $$
Commented by mr W last updated on 17/Apr/20

$${the}\:{box}\:{contains}\:\mathrm{12}\:{balls}. \\ $$$${to}\:{draw}\:{three}\:{balls}\:{from}\:{the}\:{box}\:{there} \\ $$$${are}\:{C}_{\mathrm{3}} ^{\mathrm{12}} =\mathrm{220}\:{ways}. \\ $$$${to}\:{draw}\:{three}\:{with}\:{three}\:{different} \\ $$$${colors}\:{there}\:{are}\:\mathrm{3}×\mathrm{4}×\mathrm{5}=\mathrm{60}\:{ways} \\ $$$${the}\:{probability}\:{is} \\ $$$${p}=\frac{\mathrm{60}}{\mathrm{220}}=\frac{\mathrm{3}}{\mathrm{11}} \\ $$
Commented by jagoll last updated on 17/Apr/20
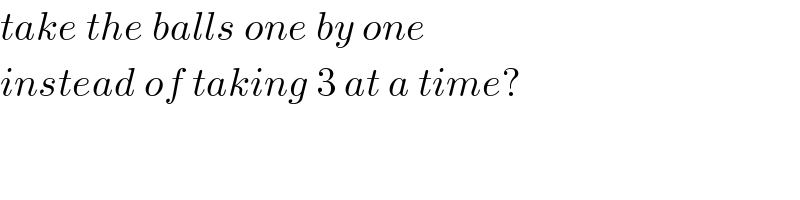
$${take}\:{the}\:{balls}\:{one}\:{by}\:{one}\: \\ $$$${instead}\:{of}\:{taking}\:\mathrm{3}\:{at}\:{a}\:{time}? \\ $$
Commented by jagoll last updated on 17/Apr/20
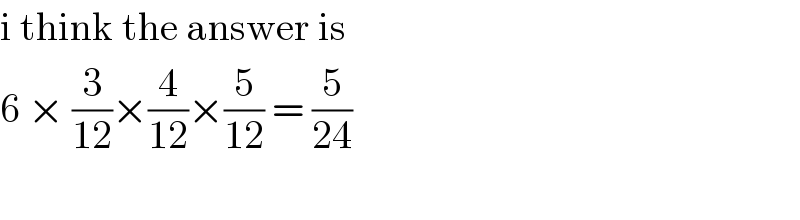
$$\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\: \\ $$$$\mathrm{6}\:×\:\frac{\mathrm{3}}{\mathrm{12}}×\frac{\mathrm{4}}{\mathrm{12}}×\frac{\mathrm{5}}{\mathrm{12}}\:=\:\frac{\mathrm{5}}{\mathrm{24}} \\ $$$$ \\ $$
