Question Number 127047 by mohammad17 last updated on 26/Dec/20
![how can graph this [x^2 +(y−1)^2 >9 ] pleas sir help me with details ?](https://www.tinkutara.com/question/Q127047.png)
$${how}\:{can}\:{graph}\:{this}\: \\ $$$$\left[{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9}\:\right]\:{pleas}\:{sir}\:{help}\:{me}\:{with}\:{details}\:? \\ $$
Answered by benjo_mathlover last updated on 26/Dec/20
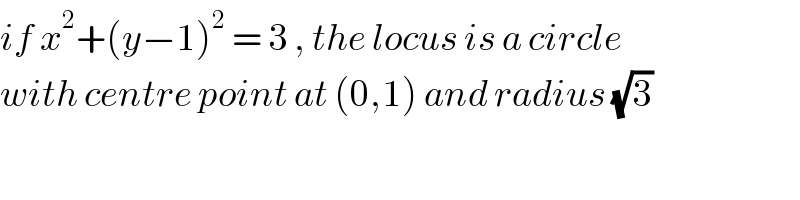
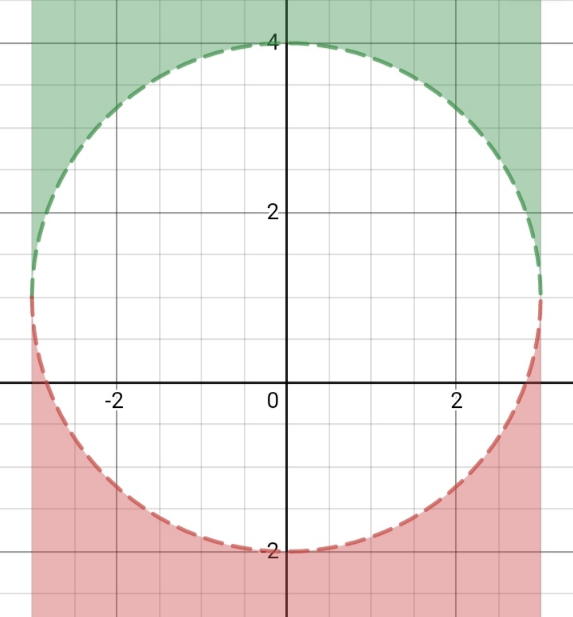
$${if}\:{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} \:=\:\mathrm{3}\:,\:{the}\:{locus}\:{is}\:{a}\:{circle} \\ $$$${with}\:{centre}\:{point}\:{at}\:\left(\mathrm{0},\mathrm{1}\right)\:{and}\:{radius}\:\sqrt{\mathrm{3}} \\ $$$$ \\ $$
Commented by mohammad17 last updated on 26/Dec/20
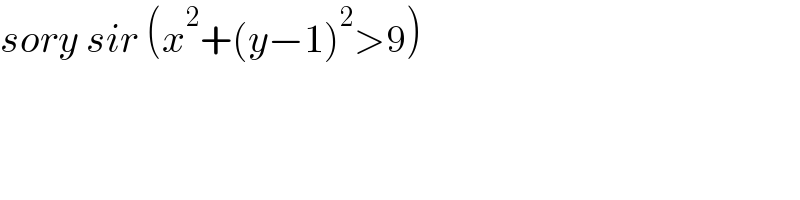
$${sory}\:{sir}\:\left({x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9}\right) \\ $$
Commented by benjo_mathlover last updated on 26/Dec/20
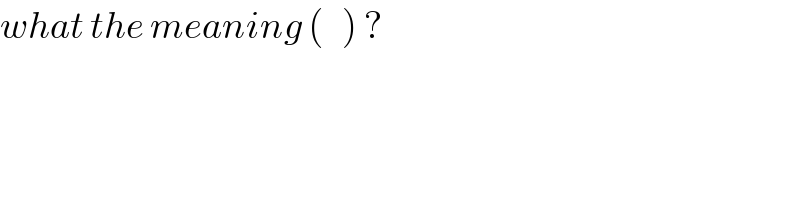
$${what}\:{the}\:{meaning}\:\left(\:\:\:\right)\:? \\ $$
Commented by mohammad17 last updated on 26/Dec/20
![[x^2 +(y−1)^2 >9]](https://www.tinkutara.com/question/Q127054.png)
$$\left[{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9}\right] \\ $$
Commented by mohammad17 last updated on 26/Dec/20
Commented by mohammad17 last updated on 26/Dec/20
![sir how the graph [x^2 +(y−1)^2 >9]it is became alssoe](https://www.tinkutara.com/question/Q127058.png)
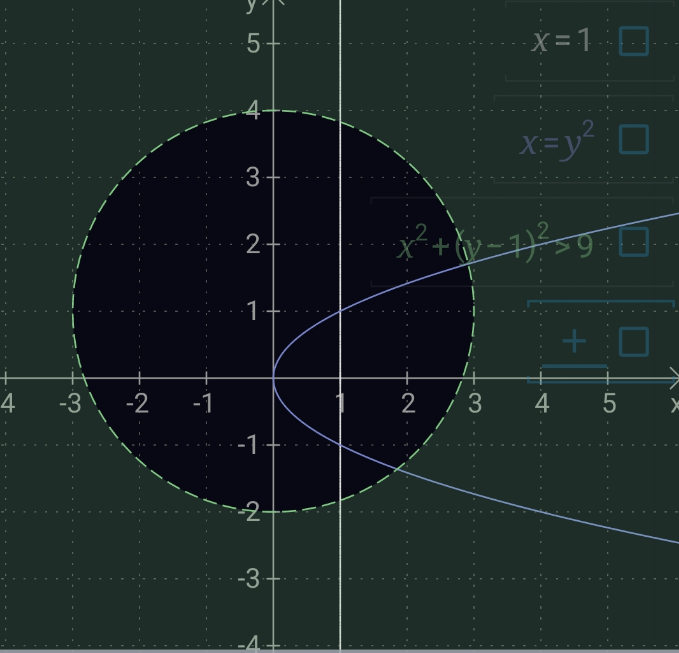
$${sir}\:{how}\:{the}\:{graph}\:\left[{x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9}\right]{it}\:{is}\:{became}\:{alssoe} \\ $$
Answered by ebi last updated on 26/Dec/20
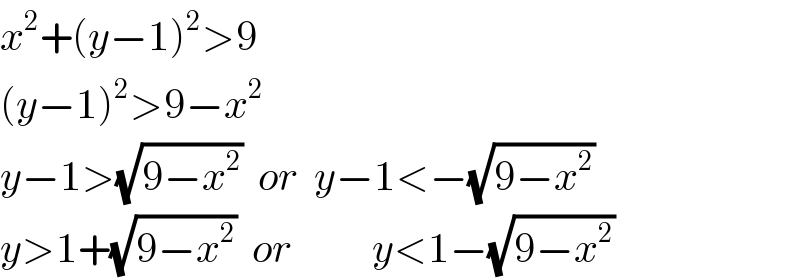
$${x}^{\mathrm{2}} +\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9} \\ $$$$\left({y}−\mathrm{1}\right)^{\mathrm{2}} >\mathrm{9}−{x}^{\mathrm{2}} \\ $$$${y}−\mathrm{1}>\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\:\:{or}\:\:{y}−\mathrm{1}<−\sqrt{\mathrm{9}−{x}^{\mathrm{2}} } \\ $$$${y}>\mathrm{1}+\sqrt{\mathrm{9}−{x}^{\mathrm{2}} }\:\:{or}\:\:\:\:\:\:\:\:\:\:{y}<\mathrm{1}−\sqrt{\mathrm{9}−{x}^{\mathrm{2}} } \\ $$
Commented by ebi last updated on 26/Dec/20