Question Number 48202 by F_Nongue last updated on 20/Nov/18
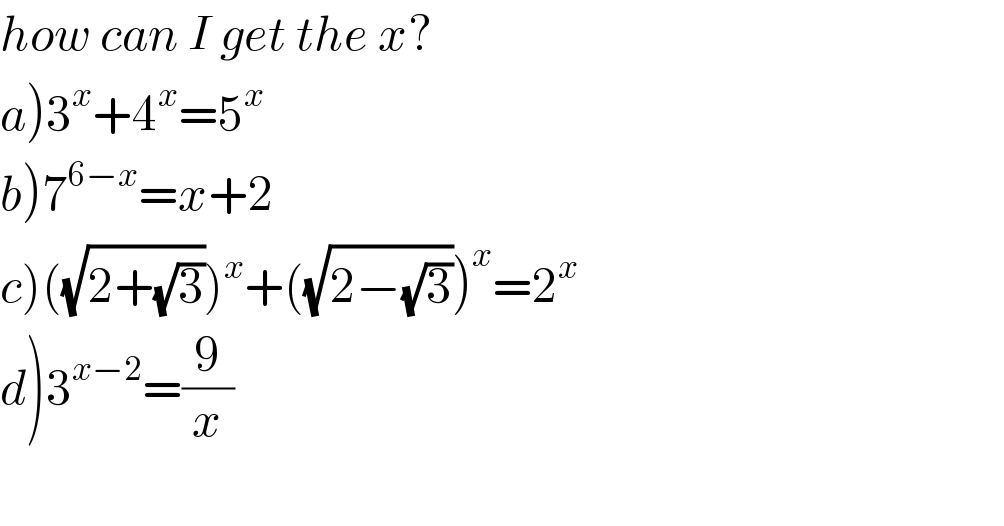
$${how}\:{can}\:{I}\:{get}\:{the}\:{x}? \\ $$$$\left.{a}\right)\mathrm{3}^{{x}} +\mathrm{4}^{{x}} =\mathrm{5}^{{x}} \\ $$$$\left.{b}\right)\mathrm{7}^{\mathrm{6}−{x}} ={x}+\mathrm{2} \\ $$$$\left.{c}\right)\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} +\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{2}^{{x}} \\ $$$$\left.{d}\right)\mathrm{3}^{{x}−\mathrm{2}} =\frac{\mathrm{9}}{{x}} \\ $$$$ \\ $$
Commented by F_Nongue last updated on 20/Nov/18
Please help
Answered by MJS last updated on 21/Nov/18
![first, try to find obvious solutions (a) x=2 [because it′s a Pythagorean triple] (b) x=5 [trying x+2=7^n ] (c) x=2 [to get rid of (√3)] (d) x=3 [because 3^1 =(9/3)] second, to find if there are more solution, differentiate and approximate for tbe valued close to the solutions (a) f(x)=3^x +4^x −5^x ⇒ f′(x)=3^x ln 3 +4^x ln 4 −5^x ln 5 we find f′(x)→0 for x→−∞ f′(x)→−∞ for x→+∞ and a peak at x≈1.287 ⇒ no other solution (b) f(x)=7^(6−x) −(x+2) ⇒ f′(x)=−(7^(6−x) ln 7 +1) this is negative for x∈R ⇒ no other solution (c) f(x)=(2+(√3))^(x/2) +(2−(√3))^(x/2) −2^x ⇒ ⇒ f′(x)=((ln (2+(√3)))/2)(2+(√3))^(x/2) +((ln (2−(√3)))/2)(2+(√3))^(x/2) −2^x ln 2 this is negative for x∈R ⇒ no other solution (d) f(x)=3^(x−2) −(9/x) ⇒ f′(x)=3^(x−2) ln 3 +(9/x^2 ) this is positive for x∈R\{0} ⇒ no other solution](https://www.tinkutara.com/question/Q48218.png)
$$\mathrm{first},\:\mathrm{try}\:\mathrm{to}\:\mathrm{find}\:\mathrm{obvious}\:\mathrm{solutions} \\ $$$$\left({a}\right)\:{x}=\mathrm{2}\:\left[\mathrm{because}\:\mathrm{it}'\mathrm{s}\:\mathrm{a}\:\mathrm{Pythagorean}\:\mathrm{triple}\right] \\ $$$$\left({b}\right)\:{x}=\mathrm{5}\:\left[\mathrm{trying}\:{x}+\mathrm{2}=\mathrm{7}^{{n}} \right] \\ $$$$\left({c}\right)\:{x}=\mathrm{2}\:\left[\mathrm{to}\:\mathrm{get}\:\mathrm{rid}\:\mathrm{of}\:\sqrt{\mathrm{3}}\right] \\ $$$$\left({d}\right)\:{x}=\mathrm{3}\:\left[\mathrm{because}\:\mathrm{3}^{\mathrm{1}} =\frac{\mathrm{9}}{\mathrm{3}}\right] \\ $$$$\mathrm{second},\:\mathrm{to}\:\mathrm{find}\:\mathrm{if}\:\mathrm{there}\:\mathrm{are}\:\mathrm{more}\:\mathrm{solution}, \\ $$$$\mathrm{differentiate}\:\mathrm{and}\:\mathrm{approximate}\:\mathrm{for}\:\mathrm{tbe}\:\mathrm{valued} \\ $$$$\mathrm{close}\:\mathrm{to}\:\mathrm{the}\:\mathrm{solutions} \\ $$$$\left({a}\right)\:{f}\left({x}\right)=\mathrm{3}^{{x}} +\mathrm{4}^{{x}} −\mathrm{5}^{{x}} \:\Rightarrow\:{f}'\left({x}\right)=\mathrm{3}^{{x}} \mathrm{ln}\:\mathrm{3}\:+\mathrm{4}^{{x}} \mathrm{ln}\:\mathrm{4}\:−\mathrm{5}^{{x}} \mathrm{ln}\:\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{we}\:\mathrm{find}\:{f}'\left({x}\right)\rightarrow\mathrm{0}\:\mathrm{for}\:{x}\rightarrow−\infty \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}'\left({x}\right)\rightarrow−\infty\:\mathrm{for}\:{x}\rightarrow+\infty \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{and}\:\mathrm{a}\:\mathrm{peak}\:\mathrm{at}\:{x}\approx\mathrm{1}.\mathrm{287}\:\Rightarrow\:\mathrm{no}\:\mathrm{other}\:\mathrm{solution} \\ $$$$\left({b}\right)\:{f}\left({x}\right)=\mathrm{7}^{\mathrm{6}−{x}} −\left({x}+\mathrm{2}\right)\:\Rightarrow\:{f}'\left({x}\right)=−\left(\mathrm{7}^{\mathrm{6}−{x}} \mathrm{ln}\:\mathrm{7}\:+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{this}\:\mathrm{is}\:\mathrm{negative}\:\mathrm{for}\:{x}\in\mathbb{R}\:\Rightarrow\:\mathrm{no}\:\mathrm{other}\:\mathrm{solution} \\ $$$$\left({c}\right)\:{f}\left({x}\right)=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} −\mathrm{2}^{{x}} \:\Rightarrow \\ $$$$\:\:\:\:\:\:\:\:\:\:\Rightarrow\:{f}'\left({x}\right)=\frac{\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{\mathrm{2}}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} +\frac{\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\mathrm{2}}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} −\mathrm{2}^{{x}} \mathrm{ln}\:\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{this}\:\mathrm{is}\:\mathrm{negative}\:\mathrm{for}\:{x}\in\mathbb{R}\:\Rightarrow\:\mathrm{no}\:\mathrm{other}\:\mathrm{solution} \\ $$$$\left({d}\right)\:{f}\left({x}\right)=\mathrm{3}^{{x}−\mathrm{2}} −\frac{\mathrm{9}}{{x}}\:\Rightarrow\:{f}'\left({x}\right)=\mathrm{3}^{{x}−\mathrm{2}} \mathrm{ln}\:\mathrm{3}\:+\frac{\mathrm{9}}{{x}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\mathrm{this}\:\mathrm{is}\:\mathrm{positive}\:\mathrm{for}\:{x}\in\mathbb{R}\backslash\left\{\mathrm{0}\right\}\:\Rightarrow\:\mathrm{no}\:\mathrm{other}\:\mathrm{solution} \\ $$
Commented by Cheyboy last updated on 21/Nov/18

$$\mathrm{Nice}\:\mathrm{Sir} \\ $$
Commented by F_Nongue last updated on 21/Nov/18
thanks sir.
