How-do-you-all-to-prove-is-true-or-false-Prove-the-1-1-p-p-2-p-3-1-1-q-q-2-q-3-1-1-r-r-2-r-3-1-1-s-s-2-s-3-1-

Question Number 164451 by Zaynal last updated on 17/Jan/22

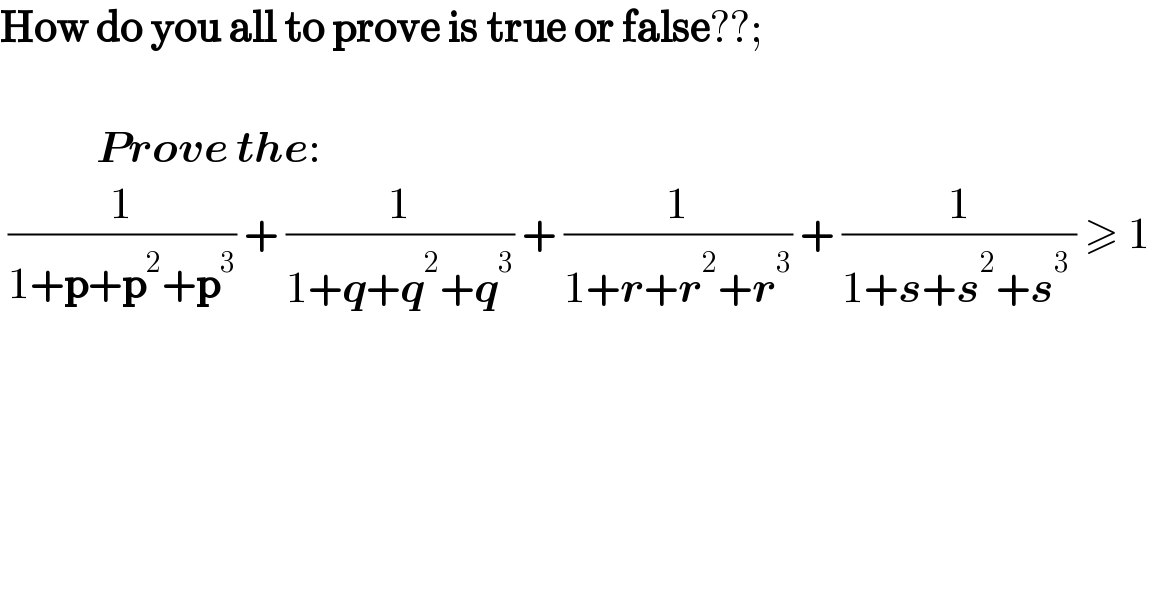
$$\boldsymbol{\mathrm{How}}\:\boldsymbol{\mathrm{do}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{all}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{prove}}\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{true}}\:\boldsymbol{\mathrm{or}}\:\boldsymbol{\mathrm{false}}??; \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{Prove}}\:\boldsymbol{{the}}: \\ $$$$\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{p}}+\boldsymbol{\mathrm{p}}^{\mathrm{2}} +\boldsymbol{\mathrm{p}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{q}}+\boldsymbol{{q}}^{\mathrm{2}} +\boldsymbol{{q}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{r}}+\boldsymbol{{r}}^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{s}}+\boldsymbol{{s}}^{\mathrm{2}} +\boldsymbol{{s}}^{\mathrm{3}\:} }\:\geqslant\:\mathrm{1} \\ $$

Commented by mr W last updated on 17/Jan/22

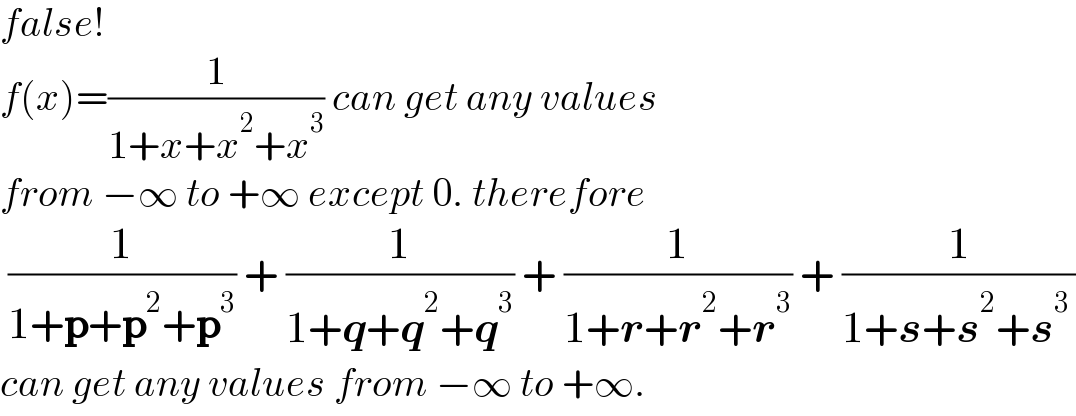
$${false}! \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} }\:{can}\:{get}\:{any}\:{values} \\ $$$${from}\:−\infty\:{to}\:+\infty\:{except}\:\mathrm{0}.\:{therefore} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{\mathrm{p}}+\boldsymbol{\mathrm{p}}^{\mathrm{2}} +\boldsymbol{\mathrm{p}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{q}}+\boldsymbol{{q}}^{\mathrm{2}} +\boldsymbol{{q}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{r}}+\boldsymbol{{r}}^{\mathrm{2}} +\boldsymbol{{r}}^{\mathrm{3}} }\:+\:\frac{\mathrm{1}}{\mathrm{1}+\boldsymbol{{s}}+\boldsymbol{{s}}^{\mathrm{2}} +\boldsymbol{{s}}^{\mathrm{3}\:} } \\ $$$${can}\:{get}\:{any}\:{values}\:{from}\:−\infty\:{to}\:+\infty. \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com