Question Number 41753 by Necxx last updated on 12/Aug/18

$${How}\:{far}\:{must}\:{a}\:{man}\:{stand}\:{in}\:{front} \\ $$$${of}\:{a}\:{concave}\:{mirror}\:{of}\:{radius}\:\mathrm{120}{cm} \\ $$$${in}\:{order}\:{to}\:{see}\:{an}\:{erect}\:{image}\:{of} \\ $$$${his}\:{face}\:{four}\:{times}\:{its}\:{actual}\:{size}? \\ $$
Answered by ajfour last updated on 12/Aug/18
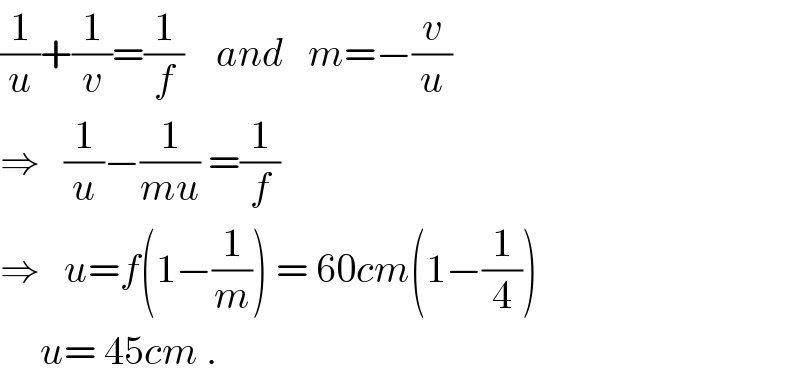
$$\frac{\mathrm{1}}{{u}}+\frac{\mathrm{1}}{{v}}=\frac{\mathrm{1}}{{f}}\:\:\:\:{and}\:\:\:{m}=−\frac{{v}}{{u}} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{1}}{{u}}−\frac{\mathrm{1}}{{mu}}\:=\frac{\mathrm{1}}{{f}} \\ $$$$\Rightarrow\:\:\:{u}={f}\left(\mathrm{1}−\frac{\mathrm{1}}{{m}}\right)\:=\:\mathrm{60}{cm}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$\:\:\:\:\:{u}=\:\mathrm{45}{cm}\:. \\ $$
Commented by Necxx last updated on 12/Aug/18

$${thank}\:{you}\:{sir} \\ $$
Answered by alex041103 last updated on 12/Aug/18
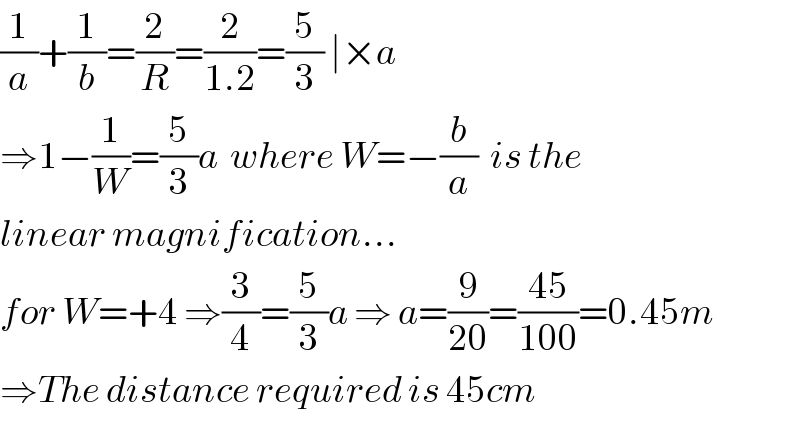
$$\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}=\frac{\mathrm{2}}{{R}}=\frac{\mathrm{2}}{\mathrm{1}.\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{3}}\:\mid×{a} \\ $$$$\Rightarrow\mathrm{1}−\frac{\mathrm{1}}{{W}}=\frac{\mathrm{5}}{\mathrm{3}}{a}\:\:{where}\:{W}=−\frac{{b}}{{a}}\:\:{is}\:{the}\: \\ $$$${linear}\:{magnification}… \\ $$$${for}\:{W}=+\mathrm{4}\:\Rightarrow\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{5}}{\mathrm{3}}{a}\:\Rightarrow\:{a}=\frac{\mathrm{9}}{\mathrm{20}}=\frac{\mathrm{45}}{\mathrm{100}}=\mathrm{0}.\mathrm{45}{m} \\ $$$$\Rightarrow{The}\:{distance}\:{required}\:{is}\:\mathrm{45}{cm} \\ $$
Commented by Necxx last updated on 12/Aug/18

$${Thank}\:{you}\:{sir} \\ $$
