Question Number 22623 by tawa tawa last updated on 21/Oct/17
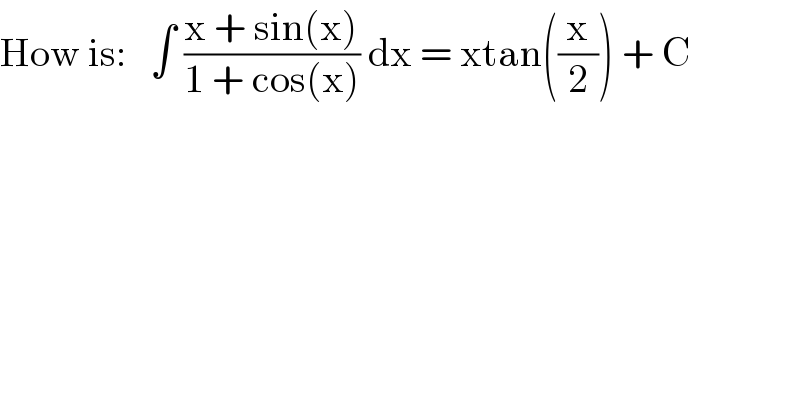
$$\mathrm{How}\:\mathrm{is}:\:\:\:\int\:\frac{\mathrm{x}\:+\:\mathrm{sin}\left(\mathrm{x}\right)}{\mathrm{1}\:+\:\mathrm{cos}\left(\mathrm{x}\right)}\:\mathrm{dx}\:=\:\mathrm{xtan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\:+\:\mathrm{C} \\ $$
Answered by vajpaithegrate@gmail.com last updated on 21/Oct/17
![∫((x+2sin (x/2)cos (x/2))/(2cos^2 (x/2)))dx ∫(x/(2cos^2 (x/2)))+((2sin (x/2)cos (x/2))/(2cos^2 (x/2))) =∫(x/2)sec^2 (x/2)+tan (x/2)dx =∫d(xtan ((x/2)))dx =xtan(x/2)+c [sin x=2sin (x/2)cos (x/2);1+cos x=2cos^2 (x/2)]](https://www.tinkutara.com/question/Q22630.png)
$$\int\frac{\mathrm{x}+\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}\mathrm{dx}\:\: \\ $$$$\int\frac{\mathrm{x}}{\mathrm{2cos}^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}}+\frac{\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}}}{\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}} \\ $$$$=\int\frac{\mathrm{x}}{\mathrm{2}}\mathrm{sec}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}+\mathrm{tan}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{dx} \\ $$$$=\int\mathrm{d}\left(\mathrm{xtan}\:\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)\mathrm{dx} \\ $$$$=\mathrm{xtan}\frac{\mathrm{x}}{\mathrm{2}}+\mathrm{c} \\ $$$$\left[\mathrm{sin}\:\mathrm{x}=\mathrm{2sin}\:\frac{\mathrm{x}}{\mathrm{2}}\mathrm{cos}\:\frac{\mathrm{x}}{\mathrm{2}};\mathrm{1}+\mathrm{cos}\:\mathrm{x}=\mathrm{2cos}\:^{\mathrm{2}} \frac{\mathrm{x}}{\mathrm{2}}\right] \\ $$
Commented by tawa tawa last updated on 21/Oct/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
