How-many-3-digits-positive-integers-are-there-such-the-sum-of-the-digits-is-10-

Question Number 123681 by ZiYangLee last updated on 27/Nov/20

How many 3 - digits positive integers

are there such the sum of the digits

is 10 ?

Answered by mr W last updated on 27/Nov/20

a b c w i t h

a + b + c = 10

a = 1 . . 9

b, c = 0 . . 9

(x + x^{2} + x^{3} + \dots + x^{9}) {(1 + x + x^{2} + \dots + x^{9})}^{2}

= \frac{x (1 - x^{9}) {(1 - x^{10})}^{2}}{{(1 - x)}^{3}}

= \dots + 54 x^{10} + \dots

\Rightarrow t h e r e a r e 54 s u c h 3 d i g i t n u m b e r s .

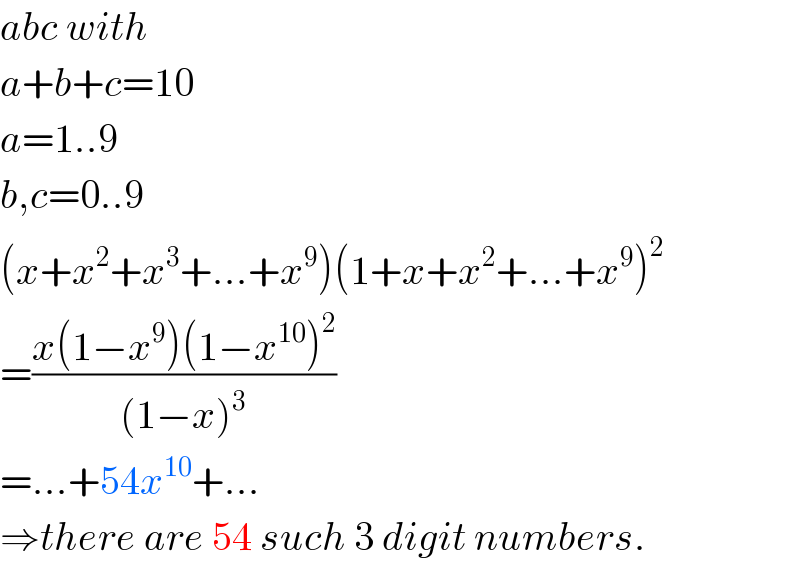
Commented by malwan last updated on 27/Nov/20

\frac{(x - x^{10}) (1 - 2 x^{10} + x^{20})}{1 - 3 x + 3 x^{2} - x^{3}}

= \frac{(x - x^{10} - 2 x^{11} + 2 x^{20} + x^{21} - x^{30})}{1 - 3 x + 3 x^{2} - x^{3}}

t h e n d i v i d e

y o u w i l l g e t \dots x^{10}

i s i t r i g h t s i r ?

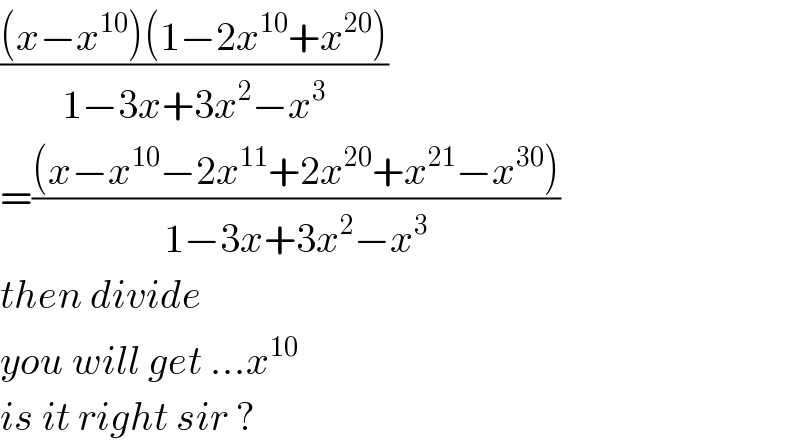
Commented by mr W last updated on 27/Nov/20

i d i d i n t h i s w a y :

\frac{1}{{(1 - x)}^{3}} = \underset{k = 0}{\sum^{\infty}} C_{2}^{k + 2} x^{k}

\frac{x (1 - x^{9}) {(1 - x^{10})}^{2}}{{(1 - x)}^{3}}

= x (1 - x^{9}) {(1 - x^{10})}^{2} \underset{k = 0}{\sum^{\infty}} C_{2}^{k + 2} x^{k}

c o e f . o f x^{10} :

C_{2}^{9 + 2} - C_{2}^{0 + 2} = C_{2}^{11} - C_{2}^{2} = \frac{11 \times 10}{2} - 1 = 54

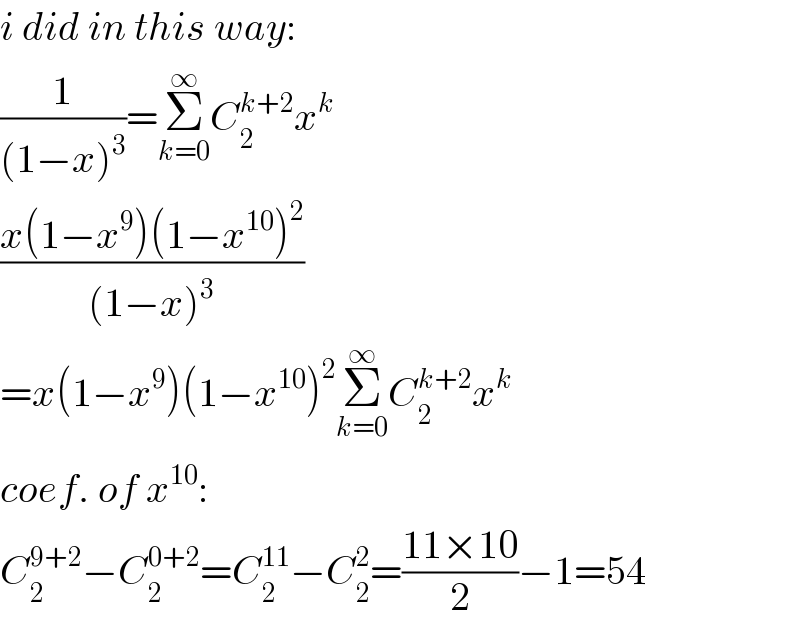
Commented by malwan last updated on 28/Nov/20

f a n t a s t i c s i r

t h a n k y o u

Answered by floor(10²Eta[1]) last updated on 27/Nov/20

109

118

127

136

145

154

163

172

181

190

(10 cases)

208

217

226

235

244

253

262

271

280

(9 cases)

307

316

325

334

343

352

361

370

(8 cases)

\dots

901

910

(2 cases)

total cases : 10 + 9 + 8 + \dots + 2 = 54