Question Number 117061 by ZiYangLee last updated on 09/Oct/20

Commented by ZiYangLee last updated on 09/Oct/20
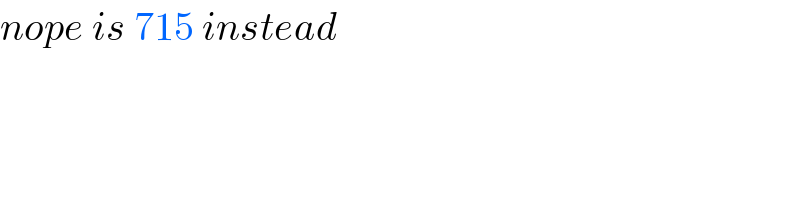
Commented by MJS_new last updated on 09/Oct/20
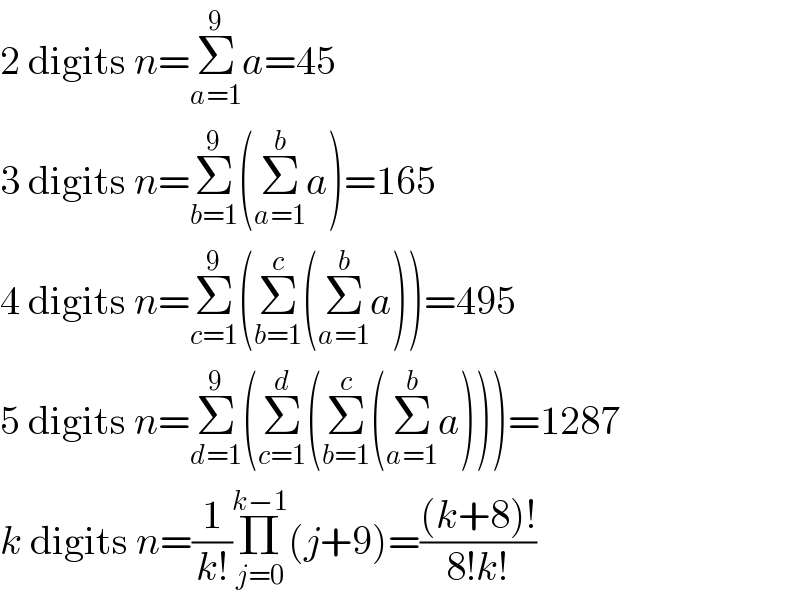
Commented by MJS_new last updated on 09/Oct/20

Answered by Olaf last updated on 09/Oct/20

Answered by mr W last updated on 11/Oct/20

Commented by mr W last updated on 11/Oct/20

