Question Number 179993 by mr W last updated on 05/Nov/22

Commented by Acem last updated on 06/Nov/22
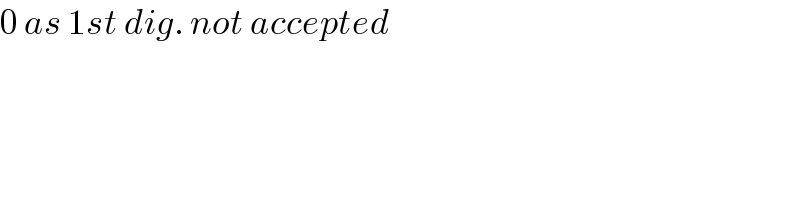
Commented by Acem last updated on 06/Nov/22

Commented by mr W last updated on 06/Nov/22

Commented by Acem last updated on 06/Nov/22
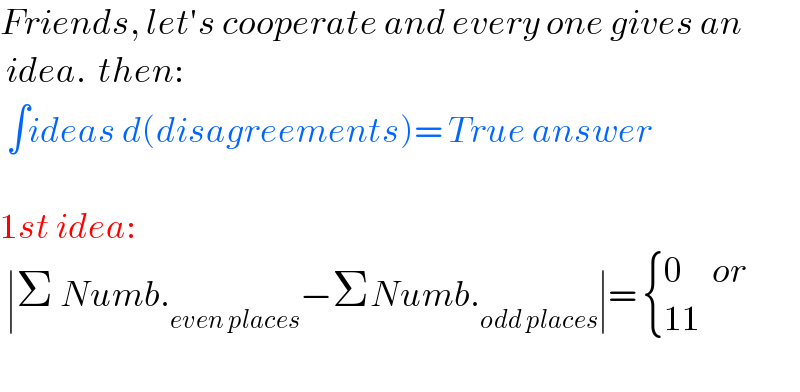
Commented by Acem last updated on 05/Nov/22

Commented by mr W last updated on 05/Nov/22

Commented by Frix last updated on 05/Nov/22

Commented by Acem last updated on 05/Nov/22
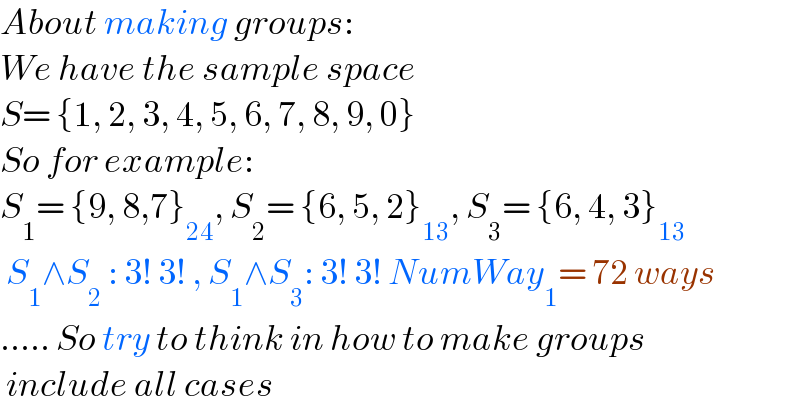
Commented by Acem last updated on 06/Nov/22
![Informations: Where do the numbers_(End_ ) ^(Start) ? Numbers ∈ [102 465, 987 635] Coefficient_(11) ∈ [9 315, 89 785] Total : 80 471 numbers are divisible by 11 ⇒ with different digits < 80 471 Primitive imagination≈ [26 555 − 28 325]](https://www.tinkutara.com/question/Q180020.png)
Commented by Rasheed.Sindhi last updated on 06/Nov/22
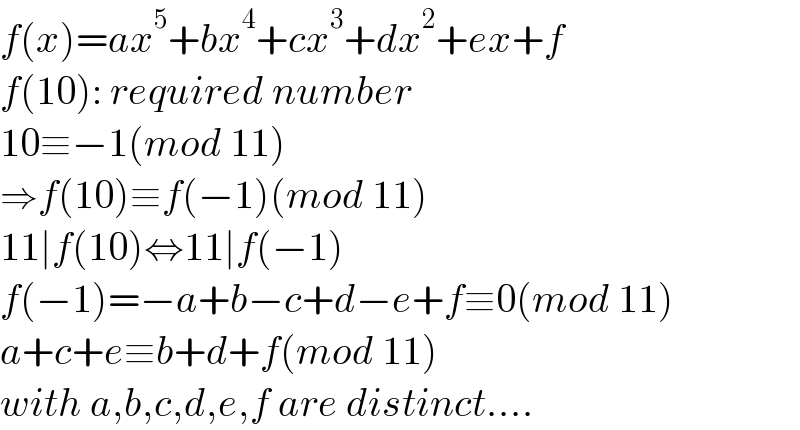
Commented by JDamian last updated on 06/Nov/22
numbers having 0 as first digit, are accepted?
Commented by nikif99 last updated on 06/Nov/22

Commented by Acem last updated on 06/Nov/22
![Yes bro , till now we didn′t know 11′s behavior, you remember the question 6 dig. divsib. by 8 it has two periodic behavior at odd hundred digits and even one, through them we sniped it. But here all what i could to do is downsizing the operations such as determine the domain Numbers ∈ [102 465, 987 635] Then i fixed two digits 98a bcd and from S={0,1,2,3,4,5,6} formed pairs as (0,1) ∧(6,7)..... (0,4)∧(2,3) .... (1,5)∧(0,7) & (3,4)... etc and i got 132 numbers (7 min of work) 2nd step 97abcd ....then 90abcd..... then 89abcd..etc sure, i didn′t continue (: But i believe that the 11 has some behaviour Thank you, and thanks for every one has tried](https://www.tinkutara.com/question/Q180047.png)
