How-many-digits-does-1000-1000-have-Mastermind-

Question Number 174928 by Mastermind last updated on 14/Aug/22

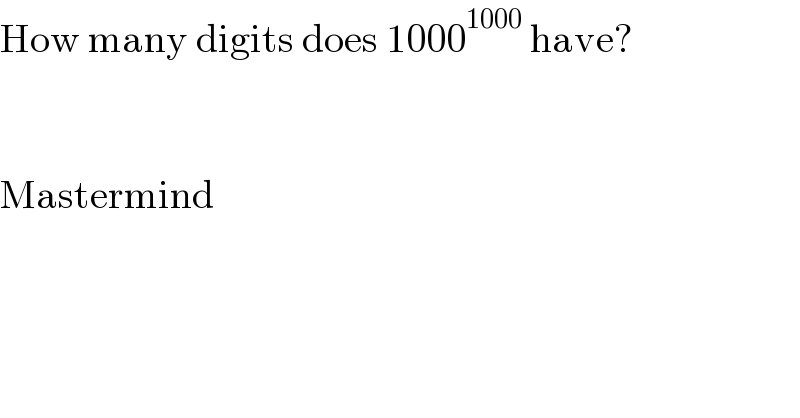
$$\mathrm{How}\:\mathrm{many}\:\mathrm{digits}\:\mathrm{does}\:\mathrm{1000}^{\mathrm{1000}} \:\mathrm{have}? \\ $$$$ \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Answered by Ar Brandon last updated on 14/Aug/22

$$\mathrm{3001} \\ $$

Commented by Mastermind last updated on 14/Aug/22

$$\mathrm{your}\:\mathrm{solution}\:\mathrm{pls} \\ $$

Answered by BaliramKumar last updated on 14/Aug/22

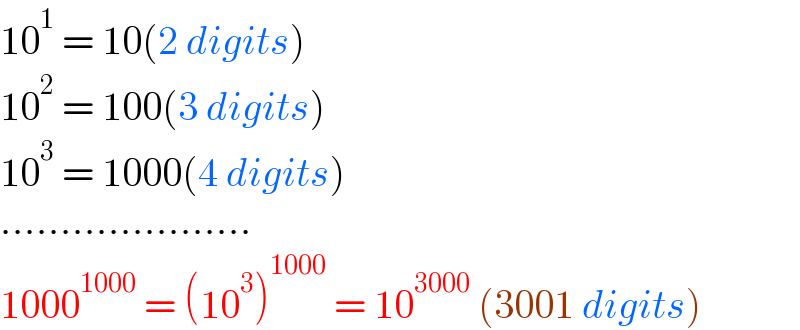
10^1 = 10(2 digits) 10^2 = 100(3 digits) 10^3 = 1000(4 digits) ..................... 1000^(1000) = (10^3 )^(1000) = 10^(3000) (3001 digits)

$$\mathrm{10}^{\mathrm{1}} \:=\:\mathrm{10}\left(\mathrm{2}\:{digits}\right) \\ $$$$\mathrm{10}^{\mathrm{2}} \:=\:\mathrm{100}\left(\mathrm{3}\:{digits}\right) \\ $$$$\mathrm{10}^{\mathrm{3}} \:=\:\mathrm{1000}\left(\mathrm{4}\:{digits}\right) \\ $$$$………………… \\ $$$$\mathrm{1000}^{\mathrm{1000}} \:=\:\left(\mathrm{10}^{\mathrm{3}} \right)^{\mathrm{1000}} \:=\:\mathrm{10}^{\mathrm{3000}} \:\left(\mathrm{3001}\:{digits}\right) \\ $$

Commented by Frix last updated on 14/Aug/22

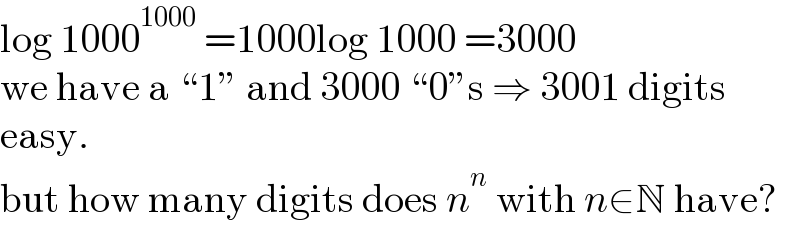
log 1000^(1000) =1000log 1000 =3000 we have a “1” and 3000 “0”s ⇒ 3001 digits easy. but how many digits does n^n with n∈N have?

$$\mathrm{log}\:\mathrm{1000}^{\mathrm{1000}} \:=\mathrm{1000log}\:\mathrm{1000}\:=\mathrm{3000} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{a}\:“\mathrm{1}''\:\mathrm{and}\:\mathrm{3000}\:“\mathrm{0}''\mathrm{s}\:\Rightarrow\:\mathrm{3001}\:\mathrm{digits} \\ $$$$\mathrm{easy}. \\ $$$$\mathrm{but}\:\mathrm{how}\:\mathrm{many}\:\mathrm{digits}\:\mathrm{does}\:{n}^{{n}} \:\mathrm{with}\:{n}\in\mathbb{N}\:\mathrm{have}? \\ $$

Commented by mr W last updated on 14/Aug/22

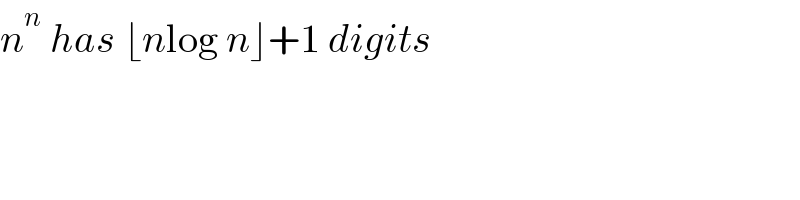
$${n}^{{n}} \:{has}\:\lfloor{n}\mathrm{log}\:{n}\rfloor+\mathrm{1}\:{digits} \\ $$

Commented by Ari last updated on 14/Aug/22

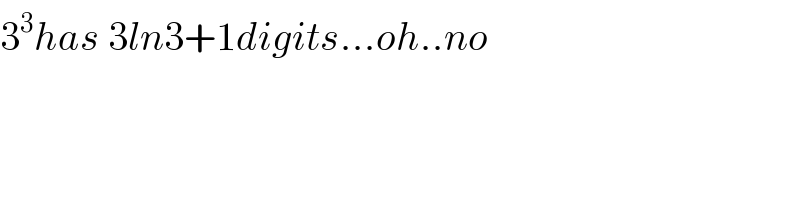
$$\mathrm{3}^{\mathrm{3}} {has}\:\mathrm{3}{ln}\mathrm{3}+\mathrm{1}{digits}…{oh}..{no} \\ $$

Commented by mr W last updated on 14/Aug/22

$${typo}! \\ $$$$\lfloor{n}\mathrm{log}\:{n}\rfloor+\mathrm{1} \\ $$

Commented by Ari last updated on 14/Aug/22

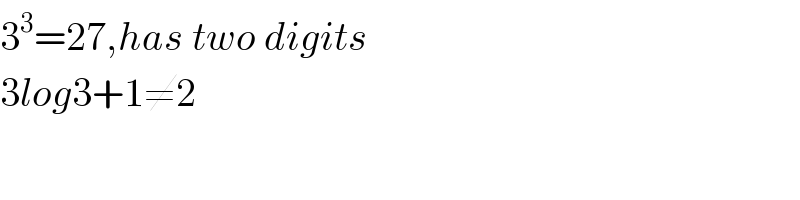
$$\mathrm{3}^{\mathrm{3}} =\mathrm{27},{has}\:{two}\:{digits} \\ $$$$\mathrm{3}{log}\mathrm{3}+\mathrm{1}\neq\mathrm{2} \\ $$

Commented by Ari last updated on 14/Aug/22

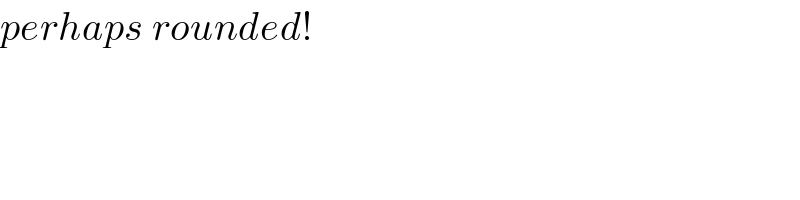
$${perhaps}\:{rounded}! \\ $$

Commented by Ari last updated on 14/Aug/22

$${take}\:{the}\:{graatest}\:{integer}\:{of}\:\left[{nlogn}\right]+\mathrm{1} \\ $$

Commented by mr W last updated on 15/Aug/22

please try to understand it before you say something is wrong! i wrote clearly ⌊nlog n⌋+1.

$${please}\:{try}\:{to}\:{understand}\:{it}\:{before} \\ $$$${you}\:{say}\:{something}\:{is}\:{wrong}! \\ $$$${i}\:{wrote}\:{clearly}\:\lfloor{n}\mathrm{log}\:{n}\rfloor+\mathrm{1}. \\ $$

Commented by Ari last updated on 15/Aug/22

$${Ok}! \\ $$

Answered by princeDera last updated on 14/Aug/22

⌊1000log (1000)⌋ + 1 = 1000⌊3log (10)⌋ + 1 = 3000+1 = 3001

$$ \\ $$$$\lfloor\mathrm{1000log}\:\:\left(\mathrm{1000}\right)\rfloor\:+\:\mathrm{1}\:=\:\mathrm{1000}\lfloor\mathrm{3log}\:\left(\mathrm{10}\right)\rfloor\:+\:\mathrm{1}\:=\:\mathrm{3000}+\mathrm{1}\:=\:\mathrm{3001} \\ $$

Commented by Ari last updated on 14/Aug/22

$${wrong}! \\ $$

Commented by princeDera last updated on 14/Aug/22

it was a mistake log_(10) and not log _e

$${it}\:{was}\:{a}\:{mistake} \\ $$$$ \\ $$$$\mathrm{log}_{\mathrm{10}} \:{and}\:{not}\:\mathrm{log}\:_{{e}} \\ $$

Facebook Tweet Pin

How-many-digits-does-1000-1000-have-Mastermind-

Leave a Reply Cancel reply