Question Number 87790 by mathocean1 last updated on 06/Apr/20

$$\mathrm{How}\:\mathrm{many}\:\mathrm{handshakes}\:\mathrm{are}\:\mathrm{exchanged} \\ $$$$\mathrm{betwen}\:\mathrm{27}\:\mathrm{boys}? \\ $$
Answered by TANMAY PANACEA. last updated on 06/Apr/20

$$\mathrm{27}{C}_{\mathrm{2}} \\ $$$$=\frac{\mathrm{27}!}{\mathrm{2}!\mathrm{25}!}=\frac{\mathrm{27}×\mathrm{26}}{\mathrm{2}}=\mathrm{351} \\ $$
Answered by Serlea last updated on 06/Apr/20
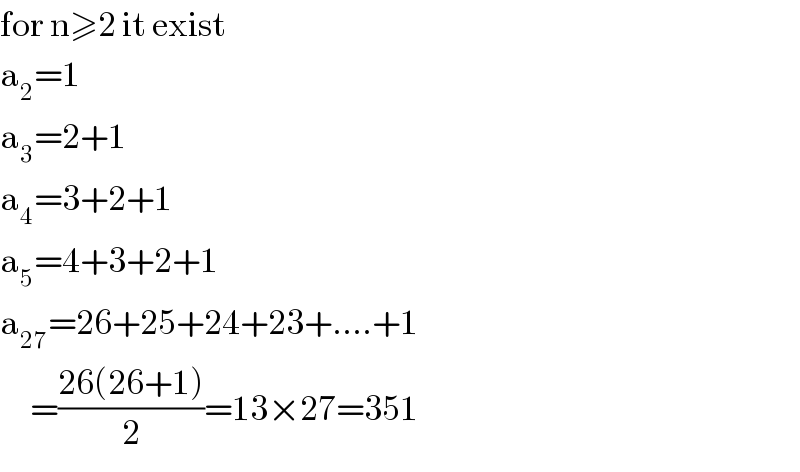
$$\mathrm{for}\:\mathrm{n}\geqslant\mathrm{2}\:\mathrm{it}\:\mathrm{exist} \\ $$$$\mathrm{a}_{\mathrm{2}} =\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{3}} =\mathrm{2}+\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{4}} =\mathrm{3}+\mathrm{2}+\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{5}} =\mathrm{4}+\mathrm{3}+\mathrm{2}+\mathrm{1} \\ $$$$\mathrm{a}_{\mathrm{27}} =\mathrm{26}+\mathrm{25}+\mathrm{24}+\mathrm{23}+….+\mathrm{1} \\ $$$$\:\:\:\:\:=\frac{\mathrm{26}\left(\mathrm{26}+\mathrm{1}\right)}{\mathrm{2}}=\mathrm{13}×\mathrm{27}=\mathrm{351} \\ $$
