Question Number 100130 by bemath last updated on 25/Jun/20

$$\mathrm{how}\:\mathrm{many}\:\mathrm{integer}\:\mathrm{number}\: \\ $$$$\mathrm{satisfy}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\frac{\mathrm{sin}\:\mathrm{x}−\mid\mathrm{x}+\mathrm{2}\mid}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{5}}\:\geqslant\:\mathrm{0}\: \\ $$
Answered by mr W last updated on 25/Jun/20
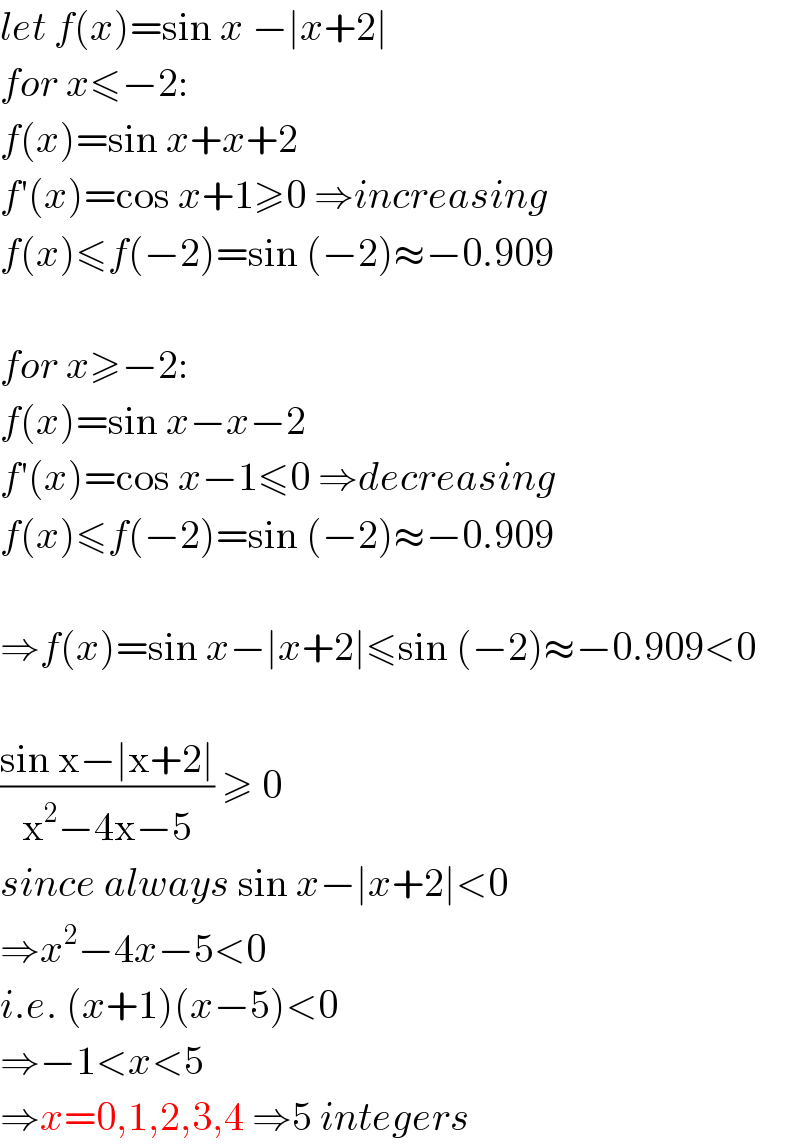
$${let}\:{f}\left({x}\right)=\mathrm{sin}\:{x}\:−\mid{x}+\mathrm{2}\mid \\ $$$${for}\:{x}\leqslant−\mathrm{2}: \\ $$$${f}\left({x}\right)=\mathrm{sin}\:{x}+{x}+\mathrm{2} \\ $$$${f}'\left({x}\right)=\mathrm{cos}\:{x}+\mathrm{1}\geqslant\mathrm{0}\:\Rightarrow{increasing} \\ $$$${f}\left({x}\right)\leqslant{f}\left(−\mathrm{2}\right)=\mathrm{sin}\:\left(−\mathrm{2}\right)\approx−\mathrm{0}.\mathrm{909} \\ $$$$ \\ $$$${for}\:{x}\geqslant−\mathrm{2}: \\ $$$${f}\left({x}\right)=\mathrm{sin}\:{x}−{x}−\mathrm{2} \\ $$$${f}'\left({x}\right)=\mathrm{cos}\:{x}−\mathrm{1}\leqslant\mathrm{0}\:\Rightarrow{decreasing} \\ $$$${f}\left({x}\right)\leqslant{f}\left(−\mathrm{2}\right)=\mathrm{sin}\:\left(−\mathrm{2}\right)\approx−\mathrm{0}.\mathrm{909} \\ $$$$ \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{sin}\:{x}−\mid{x}+\mathrm{2}\mid\leqslant\mathrm{sin}\:\left(−\mathrm{2}\right)\approx−\mathrm{0}.\mathrm{909}<\mathrm{0} \\ $$$$ \\ $$$$\frac{\mathrm{sin}\:\mathrm{x}−\mid\mathrm{x}+\mathrm{2}\mid}{\mathrm{x}^{\mathrm{2}} −\mathrm{4x}−\mathrm{5}}\:\geqslant\:\mathrm{0}\: \\ $$$${since}\:{always}\:\mathrm{sin}\:{x}−\mid{x}+\mathrm{2}\mid<\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −\mathrm{4}{x}−\mathrm{5}<\mathrm{0} \\ $$$${i}.{e}.\:\left({x}+\mathrm{1}\right)\left({x}−\mathrm{5}\right)<\mathrm{0} \\ $$$$\Rightarrow−\mathrm{1}<{x}<\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\:\Rightarrow\mathrm{5}\:{integers} \\ $$
Commented by Rasheed.Sindhi last updated on 25/Jun/20

$$\mathcal{T}_{\mathcal{H}_{\mathcal{A}} \:\mathcal{N}} {k}_{\mathcal{S}\:\:} \: \\ $$$$\:\:\:\mathcal{S}_{\mathcal{I}} \:\mathcal{R} \\ $$$$\:\:\:\:\:\:! \\ $$
Commented by bobhans last updated on 26/Jun/20

$$\mathrm{cooll}\:\mathrm{great} \\ $$
