Question Number 130034 by EDWIN88 last updated on 22/Jan/21

$$\mathrm{How}\:\mathrm{many}\:\mathrm{integers}\:\mathrm{between}\:\mathrm{999}\:\mathrm{and}\:\mathrm{4000} \\ $$$$\left(\mathrm{both}\:\mathrm{are}\:\mathrm{included}\right)\:\mathrm{can}\:\mathrm{be}\:\mathrm{formed}\:\mathrm{using} \\ $$$$\mathrm{digits}\:\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\:\mathrm{if}\:\mathrm{repetition}\:\mathrm{of}\:\mathrm{digits}\:\mathrm{is} \\ $$$$\mathrm{allowed}?\: \\ $$
Answered by liberty last updated on 22/Jan/21
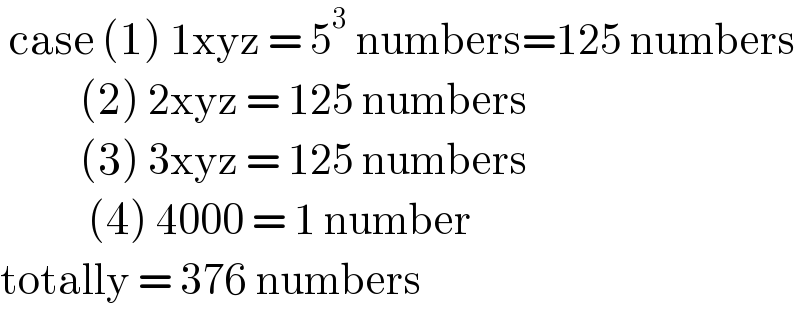
$$\:\mathrm{case}\:\left(\mathrm{1}\right)\:\mathrm{1xyz}\:=\:\mathrm{5}^{\mathrm{3}} \:\mathrm{numbers}=\mathrm{125}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right)\:\mathrm{2xyz}\:=\:\mathrm{125}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right)\:\mathrm{3xyz}\:=\:\mathrm{125}\:\mathrm{numbers} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{4}\right)\:\mathrm{4000}\:=\:\mathrm{1}\:\mathrm{number} \\ $$$$\mathrm{totally}\:=\:\mathrm{376}\:\mathrm{numbers} \\ $$
