How-many-n-digit-integers-are-divisible-by-9-

Question Number 118019 by prakash jain last updated on 14/Oct/20

How many n digit integers are

divisible by 9 ?

Commented by prakash jain last updated on 14/Oct/20

d_{1} d_{2} \dots . d_{n} is n digit number . where

d_{1}, d_{2} \dots, d_{n} are digits .

Express result in terms of n .

example for n = 2

18, 27, 36, 45, 54, 63, 72, 81, 90, 99

Commented by mr W last updated on 14/Oct/20

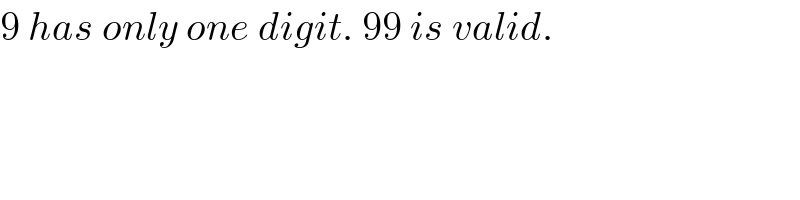
9 h a s o n l y o n e d i g i t . 99 i s v a l i d .

Commented by prakash jain last updated on 14/Oct/20

Yes . my mistake .

Answered by 1549442205PVT last updated on 14/Oct/20

It is infinite many because the condition

for a number divisible by 9 that is

the sum of its digits divisible by 9

Example : 9, 18, 108, 1008, 10008, \dots

Commented by prakash jain last updated on 14/Oct/20

Sorry about not being clear on question .

Added clarification on question

Answered by mr W last updated on 14/Oct/20

{i t}^{'} s e a s i e r t h a n o n e m a y t h i n k .

t h e f i r s t o n e i s 10^{n - 1} + 8

t h e s e c o n d o n e i s 10^{n - 1} + 17

\dots

t h e l a s t o n e i s 10^{n} - 1

t o t a l l y

\frac{(10^{n} - 1) - (10^{n - 1} - 1)}{9} = 10^{n - 1} n u m b e r s

Commented by prakash jain last updated on 14/Oct/20

Thanks .