How-many-non-similar-triangles-have-integer-angles-in-

Question Number 189021 by mr W last updated on 10/Mar/23

H o w m a n y n o n - s i m i l a r t r i a n g l e s

h a v e i n t e g e r a n g l e s i n ° ?

Commented by nikif99 last updated on 11/Mar/23

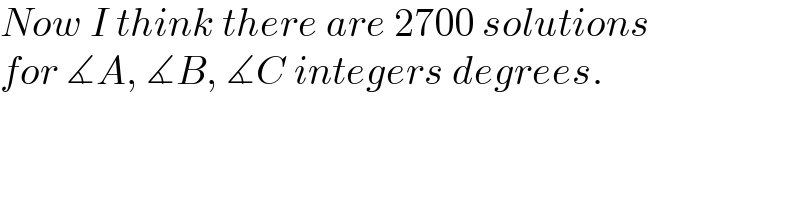
N o w I t h i n k t h e r e a r e 2700 s o l u t i o n s

f o r ∡ A, ∡ B, ∡ C i n t e g e r s d e g r e e s .

Commented by mr W last updated on 11/Mar/23

{t h a t}^{'} s c o r r e c t . c a n y o u s h a r e h o w

y o u g o t t h i s r e s u l t ?

Commented by nikif99 last updated on 11/Mar/23

∡ A t a k e s v a l u e s 1 t o 60 (t o a v o i d

c i r c u l a r r e p e t i t i o n s), ∡ B t a k e s

v a l u e s f r o m A t o i n t (\frac{180 - A}{2}) a n d

∡ C t h e r e s t t i l l 180 .

∡ A = 1 ∡ B = 1 t o 89 89 c a s e s

∡ A = 2 ∡ B = 2 t o 89 88 c a s e s

∡ A = 3 ∡ B = 3 t o 88 86 c a s e s (m i s s i n g 87)

∡ A = 4 ∡ B = 4 t o 88 85 c a s e s

∡ A = 5 ∡ B = 5 t o 87 83 c a s e s (m i s s i n g 84)

\dots

∡ A = 58 ∡ B = 58 t o 61 4 c a s e s

∡ A = 59 ∡ B = 59 t o 60 2 c a s e s (m i s s i n g 3)

∡ A = 60 ∡ B = 60 t o 60 1 c a s e

\underset{n = 1}{\sum^{89}} = \frac{n (n + 1)}{2} = 4005

l e s s c a s e s 87 - 84 - 81 - \dots - 6 - 3 =

3 \underset{n = 1}{\sum^{29}} = 1305 \Rightarrow r e a l c a s e s = 4005 - 1305 = 2700

Commented by mr W last updated on 11/Mar/23

t h a n k s a l o t f o r y o u r n i c e s o l u t i o n!

Answered by nikif99 last updated on 11/Mar/23

675 f o u n d u s i n g

\sin A + \sin B + \sin C = 4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}

a n d t r i a n g l e i n e q u a l i t i e s .

Commented by mr W last updated on 11/Mar/23

p l e a s e e x p l a i n a l i t t l e m o r e!

t h e a n g l e s o f t h e t r i a n g l e s h o u l d b e

i n t e g e r s, e . g . 1 ° + 2 ° + 177 ° i s s u c h a

t r i a n g l e .

Commented by nikif99 last updated on 11/Mar/23

p l e a s e l e t m e e x a m i n e i t a l i t t l e m o r e .

i t s e e m s t h e r e a r e e r r o r s .

Answered by mr W last updated on 11/Mar/23

a n o t h e r m e t h o d u s i n g g e n e r a t i n g

f u n c t i o n :

α + β + γ = 180 °

w i t h 1 ° ⩽ α ⩽ β ⩽ γ

l e t

α = 1 + p w i t h p ⩾ 0

β = α + q = 1 + p + q w i t h q ⩾ 0

γ = β + r = 1 + p + q + γ w i t h r ⩾ 0

(1 + p) + (1 + p + q) + (1 + p + q + r) = 180

\Rightarrow 3 + 3 p + 2 q + r = 180 \dots (i)

w i t h p, q, r ⩾ 0

n u m b e r o f s o l u t i o n s o f (i) i s t h e

c o e f . o f t e r m x^{180} i n t h e e x p a n s i o n o f

x^{3} (1 + x^{3} + x^{6} + \dots) (1 + x^{2} + x^{4} + \dots) (1 + x + x^{2} + \dots)

= \frac{x^{3}}{(1 - x^{3}) (1 - x^{2}) (1 - x)}

w h i c h i s 2700 .

t h e r e f o r e t h e r e a r e 2700 t r i a n g l e s

w i t h i n t e g e r a n g l e s i n d e g r e e s .

Commented by mr W last updated on 11/Mar/23

Facebook Tweet Pin