Question Number 130685 by EDWIN88 last updated on 28/Jan/21

$${How}\:{many}\:{password}\:{containing} \\ $$$$\mathrm{6}\:{characters}\:{of}\:{the}\:{letters}\:{in}\:{the}\: \\ $$$${word}\:''\:{Move}\:{Now}\:''\:? \\ $$
Answered by liberty last updated on 28/Jan/21
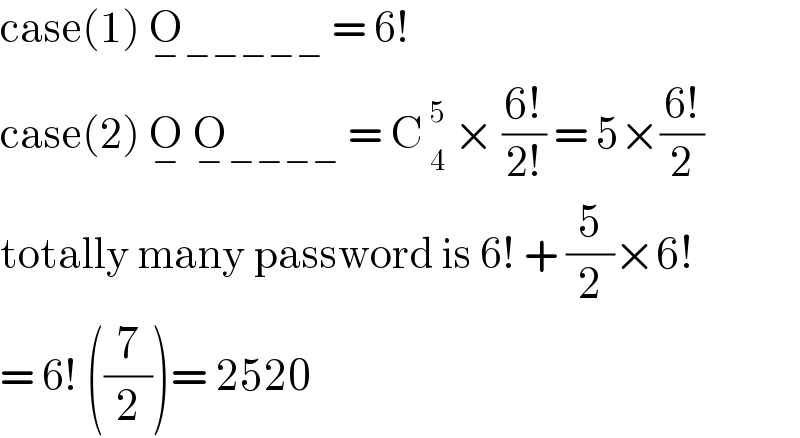
$$\mathrm{case}\left(\mathrm{1}\right)\:\underset{−} {\mathrm{O}}\underset{−} {\:}\underset{−} {\:}\underset{−} {\:}\underset{−−} {\:}\:=\:\mathrm{6}! \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\underset{−} {\mathrm{O}}\:\underset{−} {\mathrm{O}}\underset{−} {\:}\underset{−} {\:}\underset{−} {\:}\underset{−} {\:}\:=\:\mathrm{C}_{\:\mathrm{4}} ^{\:\mathrm{5}} \:×\:\frac{\mathrm{6}!}{\mathrm{2}!}\:=\:\mathrm{5}×\frac{\mathrm{6}!}{\mathrm{2}} \\ $$$$\mathrm{totally}\:\mathrm{many}\:\mathrm{password}\:\mathrm{is}\:\mathrm{6}!\:+\:\frac{\mathrm{5}}{\mathrm{2}}×\mathrm{6}! \\ $$$$=\:\mathrm{6}!\:\left(\frac{\mathrm{7}}{\mathrm{2}}\right)=\:\mathrm{2520} \\ $$
Answered by JDamian last updated on 28/Jan/21
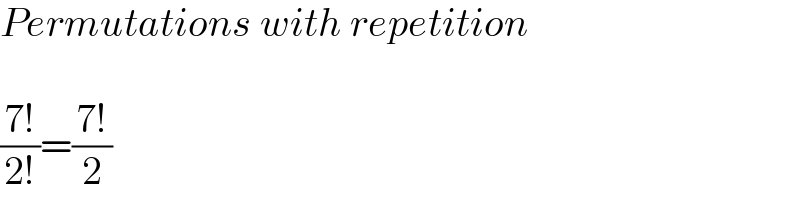
$${Permutations}\:{with}\:{repetition} \\ $$$$ \\ $$$$\frac{\mathrm{7}!}{\mathrm{2}!}=\frac{\mathrm{7}!}{\mathrm{2}} \\ $$
