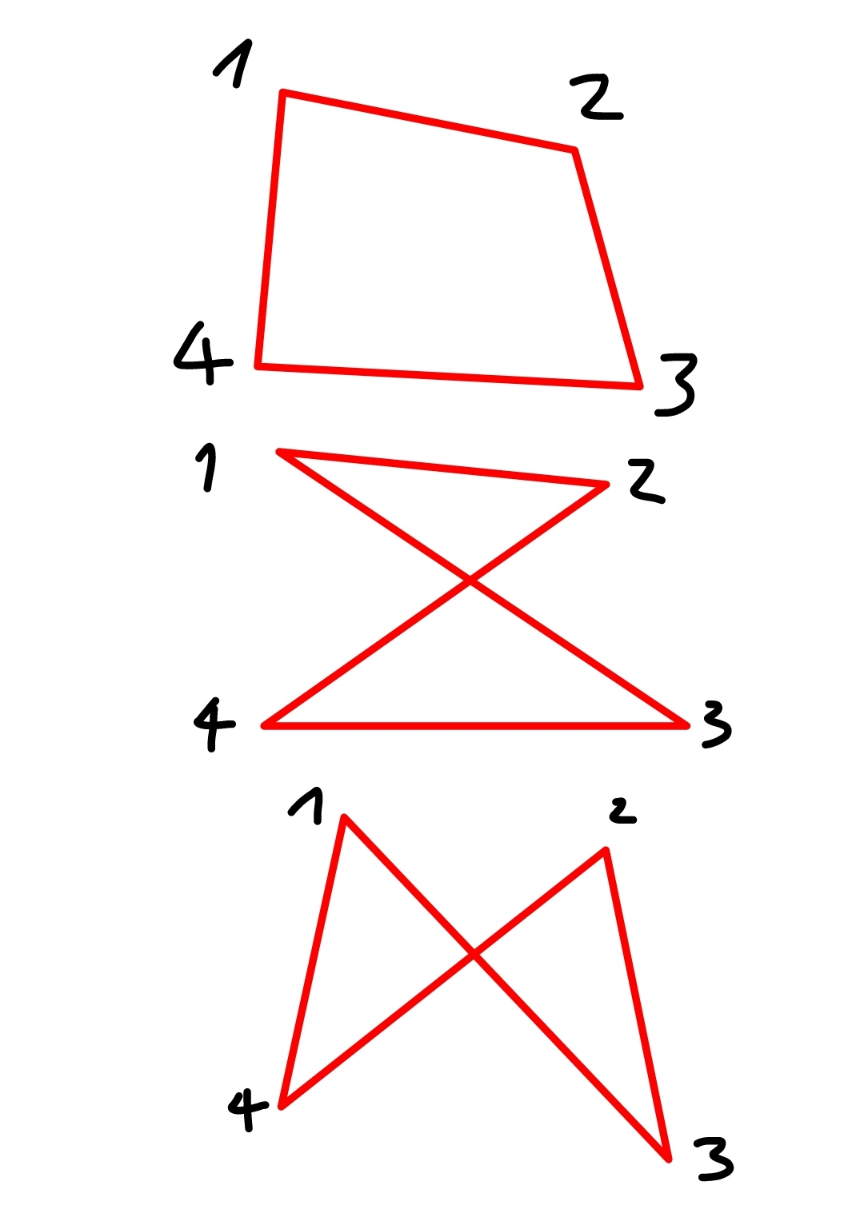
Question Number 180212 by Acem last updated on 09/Nov/22
Answered by mr W last updated on 10/Nov/22

Commented by Acem last updated on 09/Nov/22

Commented by MJS_new last updated on 09/Nov/22

Commented by Ar Brandon last updated on 09/Nov/22
You mean Dave. Lol
Commented by Frix last updated on 09/Nov/22

Commented by MJS_new last updated on 09/Nov/22

Commented by Acem last updated on 09/Nov/22

Commented by Acem last updated on 09/Nov/22

Commented by mr W last updated on 10/Nov/22

Commented by Acem last updated on 10/Nov/22

Commented by mr W last updated on 10/Nov/22

Commented by mr W last updated on 10/Nov/22