Question Number 125080 by ZiYangLee last updated on 08/Dec/20
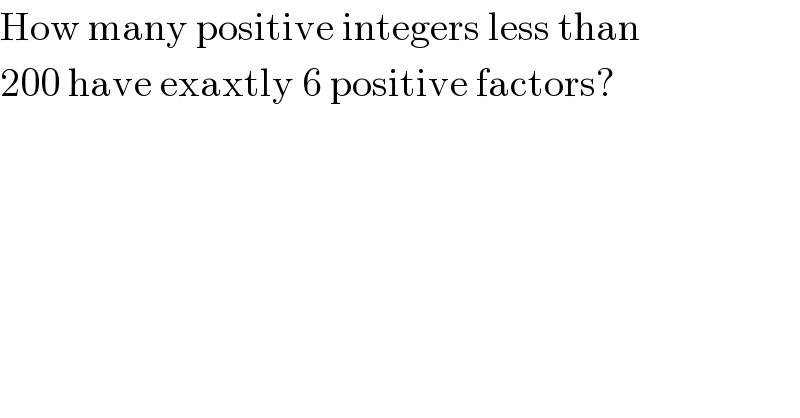
$$\mathrm{How}\:\mathrm{many}\:\mathrm{positive}\:\mathrm{integers}\:\mathrm{less}\:\mathrm{than} \\ $$$$\mathrm{200}\:\mathrm{have}\:\mathrm{exaxtly}\:\mathrm{6}\:\mathrm{positive}\:\mathrm{factors}? \\ $$
Answered by mr W last updated on 08/Dec/20
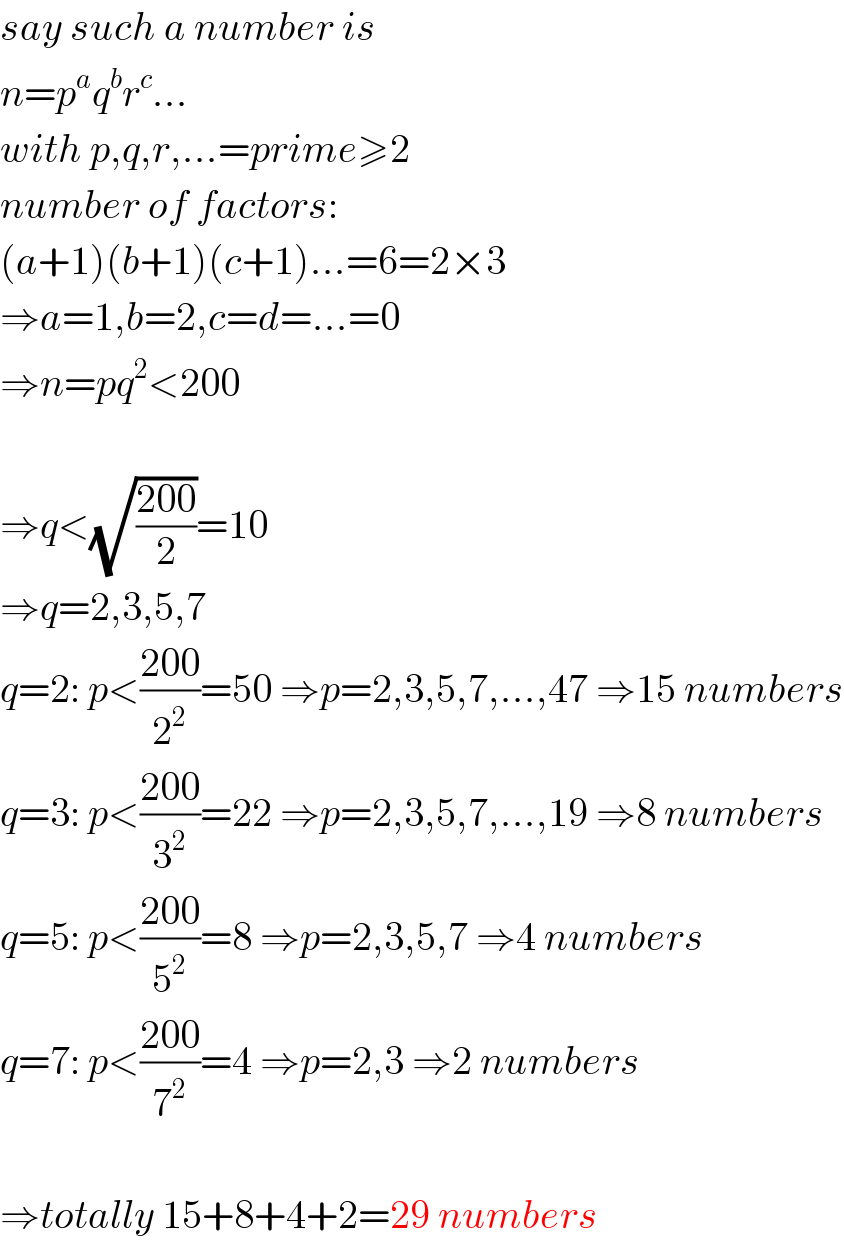
$${say}\:{such}\:{a}\:{number}\:{is} \\ $$$${n}={p}^{{a}} {q}^{{b}} {r}^{{c}} … \\ $$$${with}\:{p},{q},{r},…={prime}\geqslant\mathrm{2} \\ $$$${number}\:{of}\:{factors}: \\ $$$$\left({a}+\mathrm{1}\right)\left({b}+\mathrm{1}\right)\left({c}+\mathrm{1}\right)…=\mathrm{6}=\mathrm{2}×\mathrm{3} \\ $$$$\Rightarrow{a}=\mathrm{1},{b}=\mathrm{2},{c}={d}=…=\mathrm{0} \\ $$$$\Rightarrow{n}={pq}^{\mathrm{2}} <\mathrm{200} \\ $$$$ \\ $$$$\Rightarrow{q}<\sqrt{\frac{\mathrm{200}}{\mathrm{2}}}=\mathrm{10} \\ $$$$\Rightarrow{q}=\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7} \\ $$$${q}=\mathrm{2}:\:{p}<\frac{\mathrm{200}}{\mathrm{2}^{\mathrm{2}} }=\mathrm{50}\:\Rightarrow{p}=\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7},…,\mathrm{47}\:\Rightarrow\mathrm{15}\:{numbers} \\ $$$${q}=\mathrm{3}:\:{p}<\frac{\mathrm{200}}{\mathrm{3}^{\mathrm{2}} }=\mathrm{22}\:\Rightarrow{p}=\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7},…,\mathrm{19}\:\Rightarrow\mathrm{8}\:{numbers} \\ $$$${q}=\mathrm{5}:\:{p}<\frac{\mathrm{200}}{\mathrm{5}^{\mathrm{2}} }=\mathrm{8}\:\Rightarrow{p}=\mathrm{2},\mathrm{3},\mathrm{5},\mathrm{7}\:\Rightarrow\mathrm{4}\:{numbers} \\ $$$${q}=\mathrm{7}:\:{p}<\frac{\mathrm{200}}{\mathrm{7}^{\mathrm{2}} }=\mathrm{4}\:\Rightarrow{p}=\mathrm{2},\mathrm{3}\:\Rightarrow\mathrm{2}\:{numbers} \\ $$$$ \\ $$$$\Rightarrow{totally}\:\mathrm{15}+\mathrm{8}+\mathrm{4}+\mathrm{2}=\mathrm{29}\:{numbers} \\ $$
Commented by mr W last updated on 08/Dec/20

