How-many-real-numbers-x-satisfy-the-equation-3-2x-2-3-x-3-3-x-3-0-

Question Number 111724 by Aina Samuel Temidayo last updated on 04/Sep/20

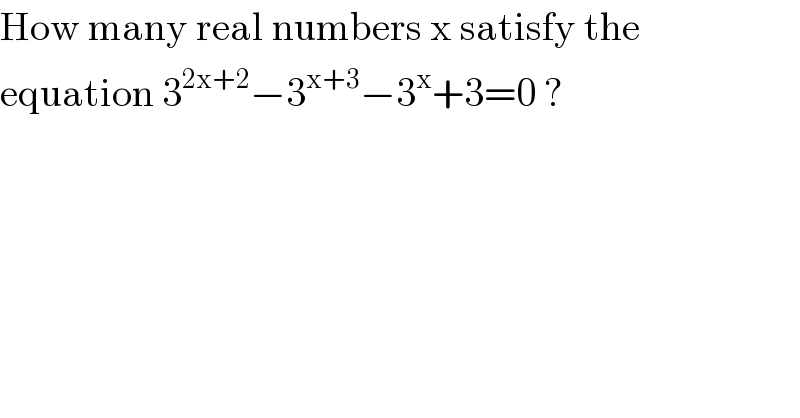
How many real numbers x satisfy the

equation 3^{2 x + 2} - 3^{x + 3} - 3^{x} + 3 = 0 ?

Commented by mohammad17 last updated on 05/Sep/20

3^{2 x} . 3^{2} - 3^{x} . 3^{3} - 3^{x} + 3 = 0

s e t : k = 3^{x}

9 k^{2} - 28 k + 3 = 0

k = \frac{- b \mp \sqrt{b^{2} - 4 a c}}{2 a} \Rightarrow k = \frac{28 \mp \sqrt{784 - 108}}{18}

k = \frac{28 \mp \sqrt{676}}{18} \Rightarrow k = \frac{28 \mp 26}{18}

e i t h e r : k = \frac{2}{18} \Rightarrow k = \frac{1}{9} \Rightarrow 3^{x} = \frac{1}{9} \Rightarrow x = \frac{l n (\frac{1}{9})}{l n (3)} \Rightarrow x = - 2

o r : k = \frac{54}{18} \Rightarrow k = 3 \Rightarrow 3^{x} = 3 \Rightarrow x = 1

∴ x = 1 i s t r u e

b y :≪ m o h a m m a d ≫

Commented by Aina Samuel Temidayo last updated on 05/Sep/20

Thanks .

Commented by Her_Majesty last updated on 05/Sep/20

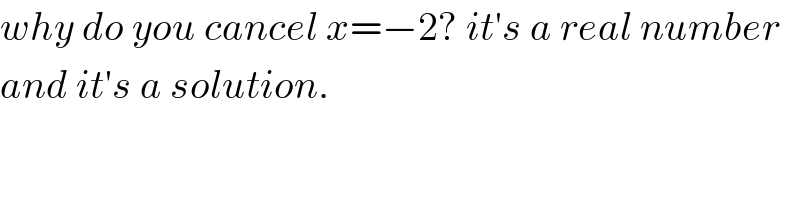
w h y d o y o u c a n c e l x = - 2 ? {i t}^{'} s a r e a l n u m b e r

a n d {i t}^{'} s a s o l u t i o n .

Commented by mohammad17 last updated on 05/Sep/20

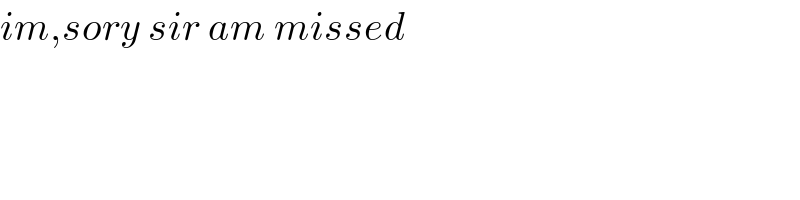
i m, s o r y s i r a m m i s s e d

Commented by mohammad17 last updated on 05/Sep/20

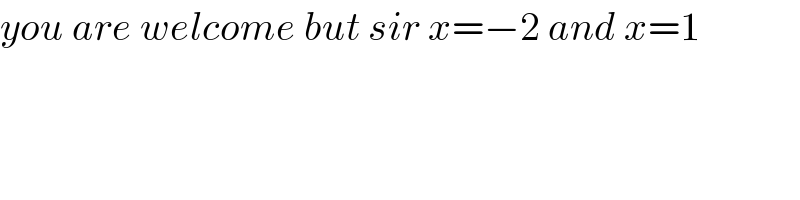
y o u a r e w e l c o m e b u t s i r x = - 2 a n d x = 1

Commented by Her_Majesty last updated on 05/Sep/20

n o w {i t}^{'} s r i g h t!