Question Number 62341 by Tawa1 last updated on 20/Jun/19
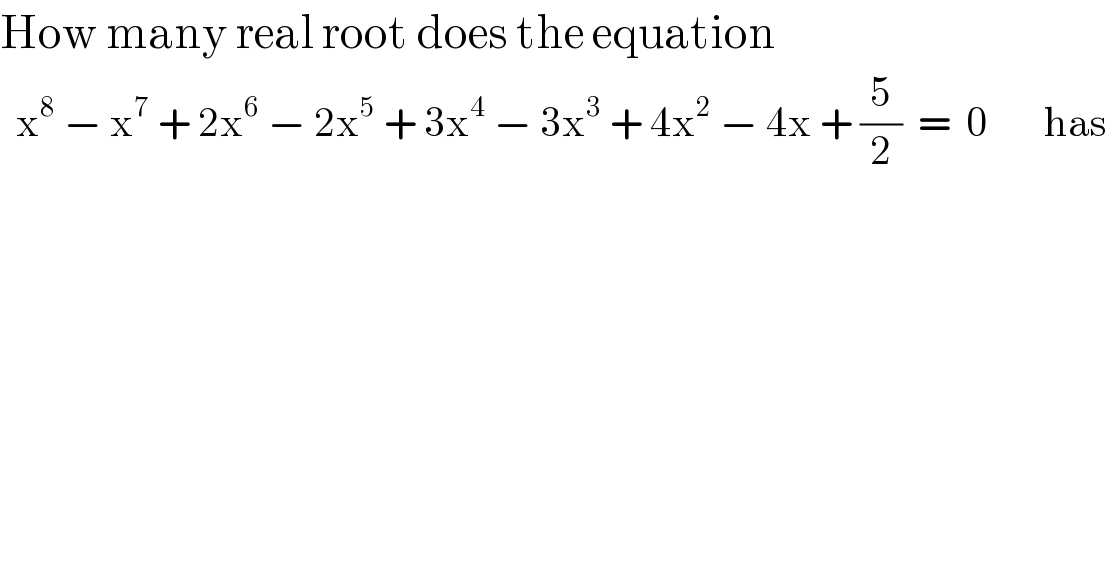
$$\mathrm{How}\:\mathrm{many}\:\mathrm{real}\:\mathrm{root}\:\mathrm{does}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\:\:\mathrm{x}^{\mathrm{8}} \:−\:\mathrm{x}^{\mathrm{7}} \:+\:\mathrm{2x}^{\mathrm{6}} \:−\:\mathrm{2x}^{\mathrm{5}} \:+\:\mathrm{3x}^{\mathrm{4}} \:−\:\mathrm{3x}^{\mathrm{3}} \:+\:\mathrm{4x}^{\mathrm{2}} \:−\:\mathrm{4x}\:+\:\frac{\mathrm{5}}{\mathrm{2}}\:\:=\:\:\mathrm{0}\:\:\:\:\:\:\:\mathrm{has} \\ $$
Commented by Kunal12588 last updated on 20/Jun/19

Commented by Kunal12588 last updated on 20/Jun/19

$${zero}\:{real}\:{roots} \\ $$
Commented by Tawa1 last updated on 20/Jun/19
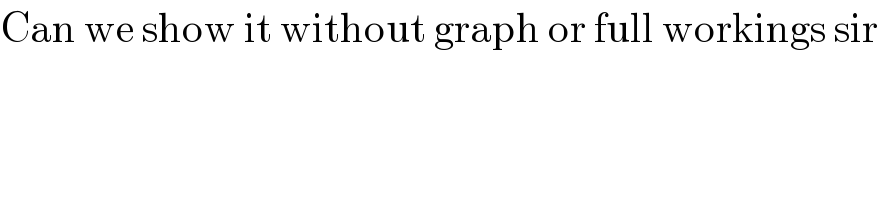
$$\mathrm{Can}\:\mathrm{we}\:\mathrm{show}\:\mathrm{it}\:\mathrm{without}\:\mathrm{graph}\:\mathrm{or}\:\mathrm{full}\:\mathrm{workings}\:\mathrm{sir} \\ $$
Answered by mr W last updated on 20/Jun/19
![f(x)= x^8 − x^7 + 2x^6 − 2x^5 + 3x^4 − 3x^3 + 4x^2 − 4x + (5/2) =(x−1)x^7 + 2(x−1)x^5 + 3(x−1)x^3 + 4(x−1)x + (5/2) =x(x−1)[x^6 + 2x^4 + 3x^2 + 4] + (5/2) =x(x−1){[(x^2 +1)^2 +2]x^2 + 4} + (5/2) ≥4x(x−1)+ (5/2) =4[(x−(1/2))^3 −(1/4)]+ (5/2) ≥4×(−(1/4))+ (5/2) =(3/2) since f(x)≥(3/2), ⇒f(x)=0 has no real roots.](https://www.tinkutara.com/question/Q62370.png)
$${f}\left({x}\right)=\:\mathrm{x}^{\mathrm{8}} \:−\:\mathrm{x}^{\mathrm{7}} \:+\:\mathrm{2x}^{\mathrm{6}} \:−\:\mathrm{2x}^{\mathrm{5}} \:+\:\mathrm{3x}^{\mathrm{4}} \:−\:\mathrm{3x}^{\mathrm{3}} \:+\:\mathrm{4x}^{\mathrm{2}} \:−\:\mathrm{4x}\:+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$=\left({x}−\mathrm{1}\right)\mathrm{x}^{\mathrm{7}} \:+\:\mathrm{2}\left({x}−\mathrm{1}\right)\mathrm{x}^{\mathrm{5}} \:+\:\mathrm{3}\left({x}−\mathrm{1}\right)\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{4}\left({x}−\mathrm{1}\right)\mathrm{x}\:+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$={x}\left({x}−\mathrm{1}\right)\left[\mathrm{x}^{\mathrm{6}} \:+\:\mathrm{2x}^{\mathrm{4}} \:+\:\mathrm{3x}^{\mathrm{2}} \:+\:\mathrm{4}\right]\:+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$={x}\left({x}−\mathrm{1}\right)\left\{\left[\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{2}\right]\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{4}\right\}\:+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\geqslant\mathrm{4}{x}\left({x}−\mathrm{1}\right)+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$=\mathrm{4}\left[\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{4}}\right]+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$\geqslant\mathrm{4}×\left(−\frac{\mathrm{1}}{\mathrm{4}}\right)+\:\frac{\mathrm{5}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$${since}\:{f}\left({x}\right)\geqslant\frac{\mathrm{3}}{\mathrm{2}}, \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{0}\:{has}\:{no}\:{real}\:{roots}. \\ $$
Commented by Tawa1 last updated on 21/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by MJS last updated on 20/Jun/19

$${x}^{\mathrm{7}} \left({x}−\mathrm{1}\right)+\mathrm{2}{x}^{\mathrm{5}} \left({x}−\mathrm{1}\right)+\mathrm{3}{x}^{\mathrm{3}} \left({x}−\mathrm{1}\right)+\mathrm{4}{x}\left({x}−\mathrm{1}\right)+\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\right)+\frac{\mathrm{5}}{\mathrm{2}}=\mathrm{0} \\ $$$$ \\ $$$${x}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\mathrm{0} \\ $$$${x}_{\mathrm{2}} =\mathrm{1} \\ $$$${g}\left({x}\right)={x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\:\mathrm{obviously}\:\mathrm{has}\:\mathrm{got}\:\mathrm{no}\:\mathrm{real} \\ $$$$\mathrm{zeros};\:\mathrm{its}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{at}\:\begin{pmatrix}{\mathrm{0}}\\{\mathrm{4}}\end{pmatrix}.\:{h}\left({x}\right)={x}\left({x}−\mathrm{1}\right)\:\mathrm{is} \\ $$$$\mathrm{a}\:\mathrm{parabola}\:\mathrm{with}\:\mathrm{minimum}\:\mathrm{at}\:\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{4}}}\end{pmatrix} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{to}\:\mathrm{seek}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{of} \\ $$$${f}\left({x}\right)={x}\left({x}−\mathrm{1}\right)\left({x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\right)\:\mathrm{with}\:\mathrm{0}<{x}<\mathrm{1} \\ $$$${f}\left(.\mathrm{4}\right)=−\mathrm{1}.\mathrm{08847104} \\ $$$${f}\left(.\mathrm{5}\right)=−\mathrm{1}.\mathrm{22265625} \\ $$$${f}\left(.\mathrm{6}\right)=−\mathrm{1}.\mathrm{29260544} \\ $$$${f}\left(.\mathrm{7}\right)=−\mathrm{1}.\mathrm{27424829} \\ $$$${f}\left(.\mathrm{65}\right)=−\mathrm{1}.\mathrm{29673}… \\ $$$${f}\left(.\mathrm{64}\right)=−\mathrm{1}.\mathrm{29785}… \\ $$$${f}\left(.\mathrm{63}\right)=−\mathrm{1}.\mathrm{29796}… \\ $$$${f}\left(.\mathrm{62}\right)=−\mathrm{1}.\mathrm{29710}… \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{close}\:\mathrm{to}\:\begin{pmatrix}{.\mathrm{63}}\\{−\mathrm{1}.\mathrm{298}}\end{pmatrix} \\ $$$$\Rightarrow\:{f}\left({x}\right)+\frac{\mathrm{5}}{\mathrm{2}}\:\mathrm{has}\:\mathrm{its}\:\mathrm{minimum}\:\mathrm{close}\:\mathrm{to} \\ $$$$\begin{pmatrix}{.\mathrm{63}}\\{\mathrm{1}.\mathrm{202}}\end{pmatrix}\:\Rightarrow\:\mathrm{it}\:\mathrm{has}\:\mathrm{no}\:\mathrm{real}\:\mathrm{zeros} \\ $$
Commented by Tawa1 last updated on 21/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
