Question Number 31670 by gunawan last updated on 12/Mar/18
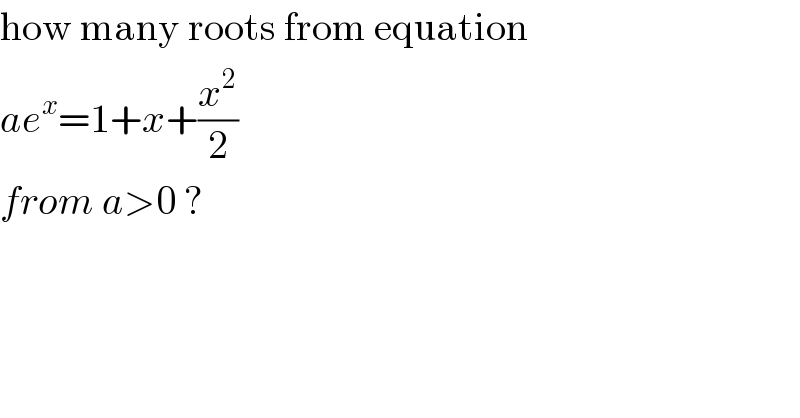
$$\mathrm{how}\:\mathrm{many}\:\mathrm{roots}\:\mathrm{from}\:\mathrm{equation} \\ $$$${ae}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${from}\:{a}>\mathrm{0}\:? \\ $$
Answered by mrW2 last updated on 12/Mar/18

$${f}\left({x}\right)={ae}^{{x}} \:\:\left({a}>\mathrm{0}\right) \\ $$$${g}\left({x}\right)=\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${with}\:{x}\rightarrow−\infty: \\ $$$${f}\left({x}\right)\rightarrow\mathrm{0},\:{g}\left({x}\right)\rightarrow+\infty \\ $$$${i}.{e}.\:{f}\left({x}\right)<{g}\left({x}\right) \\ $$$$ \\ $$$${with}\:{x}\rightarrow+\infty: \\ $$$${f}\left({x}\right)\rightarrow+\infty,\:{g}\left({x}\right)\rightarrow+\infty \\ $$$$\frac{{f}\left({x}\right)}{{g}\left({x}\right)}\rightarrow+\infty \\ $$$${i}.{e}.\:{f}\left({x}\right)>{g}\left({x}\right) \\ $$$$ \\ $$$$\Rightarrow{between}\:−\infty\:{and}\:+\infty\:{there}\:{is}\:{one} \\ $$$${intersection}\:{point}\:{from}\:{f}\left({x}\right)\:{and}\:{g}\left({x}\right), \\ $$$${i}.{e}.\:{ae}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:{has}\:{always}\:{one}\:{and} \\ $$$${only}\:{one}\:{solution}. \\ $$
Commented by gunawan last updated on 12/Mar/18
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
