Question Number 90698 by jagoll last updated on 25/Apr/20
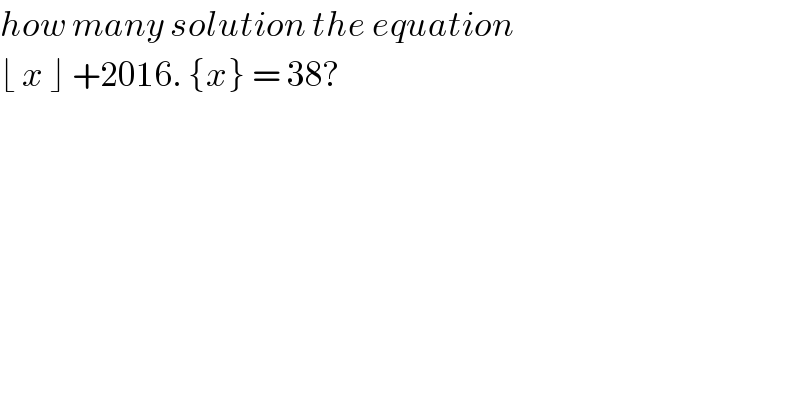
$${how}\:{many}\:{solution}\:{the}\:{equation} \\ $$$$\lfloor\:{x}\:\rfloor\:+\mathrm{2016}.\:\left\{{x}\right\}\:=\:\mathrm{38}? \\ $$
Commented by mr W last updated on 25/Apr/20

$${in}\:{general} \\ $$$$\lfloor\:{x}\:\rfloor\:+{n}\left\{{x}\right\}\:=\:{m} \\ $$$${has}\:{n}\:{solutions}. \\ $$
Commented by jagoll last updated on 25/Apr/20
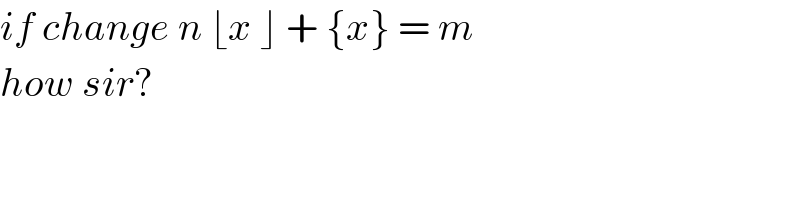
$${if}\:{change}\:{n}\:\lfloor{x}\:\rfloor\:+\:\left\{{x}\right\}\:=\:{m} \\ $$$${how}\:{sir}? \\ $$
Commented by mr W last updated on 25/Apr/20

$${it}\:{has}\:{not}\:{much}\:{sense}. \\ $$$$\left\{{x}\right\}\:{must}\:{be}\:{zero}.\:{i}.{e}.\:{x}\:{must}\:{be}\:{integer}. \\ $$$$\lfloor{x}\rfloor={x} \\ $$$${nx}={m} \\ $$$${if}\:\:{m}\equiv\mathrm{0}\:{mod}\:\left({n}\right)\:{then}\:{one}\:{solution}: \\ $$$${x}=\frac{{m}}{{n}} \\ $$$${otherwise}\:{no}\:{solution}. \\ $$
Answered by mr W last updated on 25/Apr/20
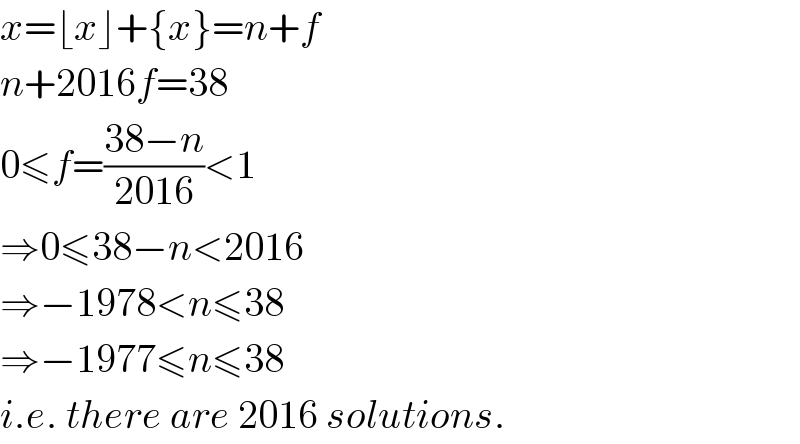
$${x}=\lfloor{x}\rfloor+\left\{{x}\right\}={n}+{f} \\ $$$${n}+\mathrm{2016}{f}=\mathrm{38} \\ $$$$\mathrm{0}\leqslant{f}=\frac{\mathrm{38}−{n}}{\mathrm{2016}}<\mathrm{1} \\ $$$$\Rightarrow\mathrm{0}\leqslant\mathrm{38}−{n}<\mathrm{2016} \\ $$$$\Rightarrow−\mathrm{1978}<{n}\leqslant\mathrm{38} \\ $$$$\Rightarrow−\mathrm{1977}\leqslant{n}\leqslant\mathrm{38} \\ $$$${i}.{e}.\:{there}\:{are}\:\mathrm{2016}\:{solutions}. \\ $$
Commented by jagoll last updated on 25/Apr/20
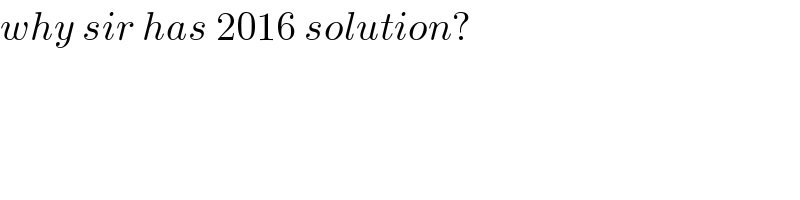
$${why}\:{sir}\:{has}\:\mathrm{2016}\:{solution}? \\ $$
Commented by mr W last updated on 25/Apr/20
![for each n ∈[−1977, 38] there is a solution x=n+((38−n)/(2016)). we have totally 2016 values of n: −1977, −1976, ...,−1, 0, 1, ..., 38 therefore there are 2016 solutions for ⌊x⌋+2016{x}=38.](https://www.tinkutara.com/question/Q90719.png)
$${for}\:{each}\:{n}\:\in\left[−\mathrm{1977},\:\mathrm{38}\right]\:{there}\:{is}\:{a} \\ $$$${solution}\:{x}={n}+\frac{\mathrm{38}−{n}}{\mathrm{2016}}. \\ $$$${we}\:{have}\:{totally}\:\mathrm{2016}\:{values}\:{of}\:{n}: \\ $$$$−\mathrm{1977},\:−\mathrm{1976},\:…,−\mathrm{1},\:\mathrm{0},\:\mathrm{1},\:…,\:\mathrm{38} \\ $$$${therefore}\:{there}\:{are}\:\mathrm{2016}\:{solutions} \\ $$$${for}\:\lfloor{x}\rfloor+\mathrm{2016}\left\{{x}\right\}=\mathrm{38}. \\ $$
Commented by jagoll last updated on 25/Apr/20
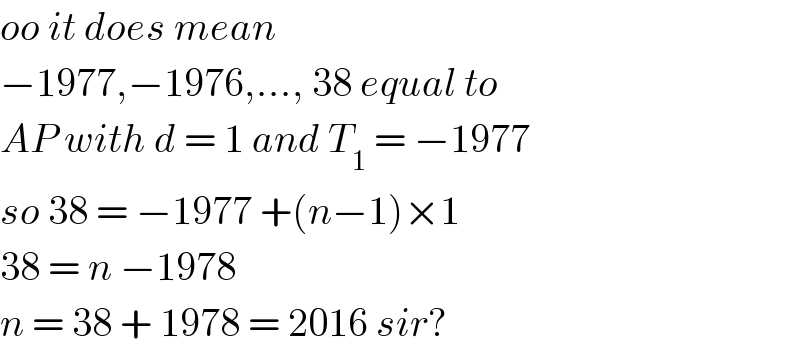
$${oo}\:{it}\:{does}\:{mean}\: \\ $$$$−\mathrm{1977},−\mathrm{1976},…,\:\mathrm{38}\:{equal}\:{to} \\ $$$${AP}\:{with}\:{d}\:=\:\mathrm{1}\:{and}\:{T}_{\mathrm{1}} \:=\:−\mathrm{1977} \\ $$$${so}\:\mathrm{38}\:=\:−\mathrm{1977}\:+\left({n}−\mathrm{1}\right)×\mathrm{1}\: \\ $$$$\mathrm{38}\:=\:{n}\:−\mathrm{1978}\: \\ $$$${n}\:=\:\mathrm{38}\:+\:\mathrm{1978}\:=\:\mathrm{2016}\:{sir}? \\ $$
Commented by mr W last updated on 25/Apr/20
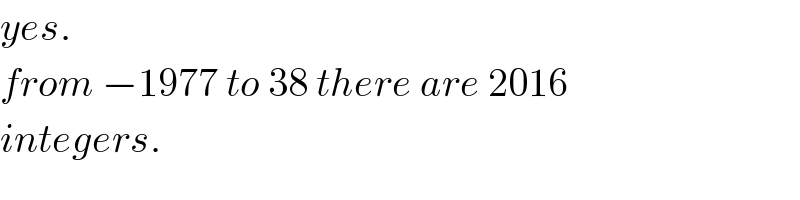
$${yes}. \\ $$$${from}\:−\mathrm{1977}\:{to}\:\mathrm{38}\:{there}\:{are}\:\mathrm{2016} \\ $$$${integers}. \\ $$
Commented by jagoll last updated on 25/Apr/20

$${thank}\:{you}\:{sir} \\ $$
