Question Number 111730 by Aina Samuel Temidayo last updated on 04/Sep/20
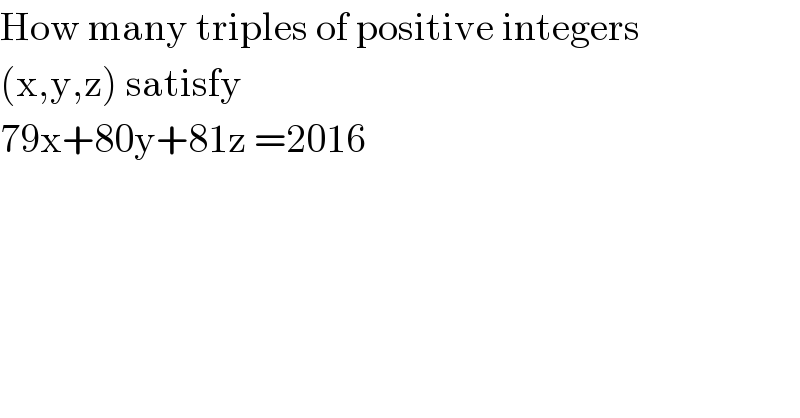
$$\mathrm{How}\:\mathrm{many}\:\mathrm{triples}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{integers} \\ $$$$\left(\mathrm{x},\mathrm{y},\mathrm{z}\right)\:\mathrm{satisfy}\: \\ $$$$\mathrm{79x}+\mathrm{80y}+\mathrm{81z}\:=\mathrm{2016} \\ $$
Commented by kaivan.ahmadi last updated on 05/Sep/20

$${let}\:{y}={t}\:{be}\:{fix} \\ $$$$ \\ $$$$\mathrm{79}{x}+\mathrm{81}{z}=\mathrm{2016}−\mathrm{80}{t}\:\:\:\left(\ast\right) \\ $$$$\mathrm{79}{x}\overset{\mathrm{81}} {\equiv}−\mathrm{9}+{t}\Rightarrow−\mathrm{2}{x}\overset{\mathrm{81}} {\equiv}−\mathrm{9}+{t}\:\:\:\:\:\:\:\overset{×\left(−\mathrm{41}\right)} {\Rightarrow}\:\:\:\: \\ $$$$\mathrm{82}{x}\overset{\mathrm{81}} {\equiv}\mathrm{369}−\mathrm{41}{t}\Rightarrow{x}\overset{\mathrm{81}} {\equiv}\mathrm{45}−\mathrm{41}{t}\Rightarrow \\ $$$${x}=\mathrm{81}{k}−\mathrm{41}{t}+\mathrm{45}\:\:\:\left({k}\in\mathbb{Z}\right)−\mathrm{79} \\ $$$${from}\:\left(\ast\right) \\ $$$$\Rightarrow\mathrm{79}\left(\mathrm{81}{k}+\mathrm{45}−\mathrm{41}{t}\right)+\mathrm{81}{z}=\mathrm{2016}−\mathrm{80}{t}\Rightarrow \\ $$$$\mathrm{81}{z}=\mathrm{81}\left(−\mathrm{79}{k}\right)+\mathrm{3159}{t}−\mathrm{1539}\Rightarrow \\ $$$${z}=−\mathrm{79}{k}+\mathrm{39}{t}−\mathrm{19} \\ $$$${x},{y},{z}\in\mathbb{N}\Rightarrow\mathrm{81}{k}−\mathrm{41}{t}+\mathrm{45}>\mathrm{0}\:,\:−\mathrm{79}{k}+\mathrm{39}{t}−\mathrm{19}>\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{41}{t}−\mathrm{45}}{\mathrm{81}}<{k}<\frac{\mathrm{39}{t}−\mathrm{19}}{\mathrm{79}} \\ $$$${if}\:{t}=\mathrm{1}\Rightarrow\frac{−\mathrm{4}}{\mathrm{81}}<{k}<\frac{\mathrm{20}}{\mathrm{79}}\Rightarrow{k}=\mathrm{0}\Rightarrow \\ $$$${x}=\mathrm{4},{y}=\mathrm{1},{z}=\mathrm{20} \\ $$$${if}\:{t}=\mathrm{2}\Rightarrow\:\frac{\mathrm{37}}{\mathrm{81}}<{k}<\frac{\mathrm{59}}{\mathrm{79}}\Rightarrow{there}\:{is}\:{no}\:{k} \\ $$$${if}\:{t}=\mathrm{3}\Rightarrow\frac{\mathrm{78}}{\mathrm{81}}<{k}<\frac{\mathrm{98}}{\mathrm{79}}\Rightarrow{k}=\mathrm{1}\Rightarrow \\ $$$${x}=\mathrm{3},{y}=\mathrm{3},{z}=\mathrm{19} \\ $$$${if}\:{t}=\mathrm{4}\Rightarrow\frac{\mathrm{119}}{\mathrm{81}}<{k}<\frac{\mathrm{137}}{\mathrm{79}}\Rightarrow{no}\:{k} \\ $$$${if}\:{t}=\mathrm{5}\Rightarrow\:\frac{\mathrm{160}}{\mathrm{81}}<{k}<\frac{\mathrm{176}}{\mathrm{79}}\Rightarrow{k}=\mathrm{2}\Rightarrow \\ $$$${x}=\mathrm{2}\:,{y}=\mathrm{5}\:,\:{z}=\mathrm{18} \\ $$$${and}\:{repeat}\:{this}\:{rule}\:{we}\:{get}\:{another}\:{answers}. \\ $$$$ \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 05/Sep/20

$${Thank}\:{you}\:{sir}.\:{You}\:{are}\:{right}. \\ $$$${I}\:{changed}\:{the}\:{answer}. \\ $$
Commented by kaivan.ahmadi last updated on 05/Sep/20
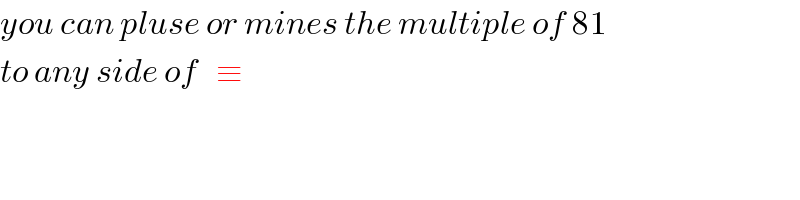
$${you}\:{can}\:{pluse}\:{or}\:{mines}\:{the}\:{multiple}\:{of}\:\mathrm{81} \\ $$$${to}\:{any}\:{side}\:{of}\:\:\:\equiv \\ $$
Commented by Aina Samuel Temidayo last updated on 05/Sep/20
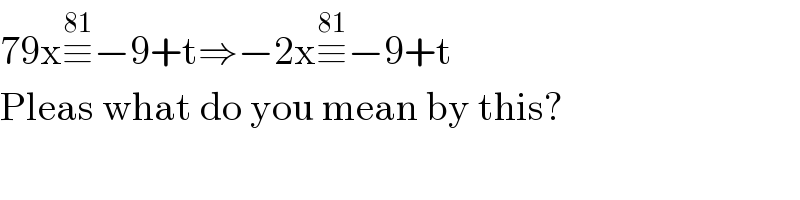
$$\mathrm{79x}\overset{\mathrm{81}} {\equiv}−\mathrm{9}+\mathrm{t}\Rightarrow−\mathrm{2x}\overset{\mathrm{81}} {\equiv}−\mathrm{9}+\mathrm{t} \\ $$$$\mathrm{Pleas}\:\mathrm{what}\:\mathrm{do}\:\mathrm{you}\:\mathrm{mean}\:\mathrm{by}\:\mathrm{this}? \\ $$
Commented by kaivan.ahmadi last updated on 05/Sep/20

$$\mathrm{79}{x}−\mathrm{81}{x}\overset{\mathrm{81}} {\equiv}−\mathrm{9}+{t} \\ $$
Commented by Rasheed.Sindhi last updated on 05/Sep/20

$$@{kivan}\:{ahmadi} \\ $$$$\left(\mathrm{1},\mathrm{7},\mathrm{17}\right)\:{also}\:{satisfy}. \\ $$$${Please}\:{review}\:{your}\:{answer}\:{there} \\ $$$${might}\:{be}\:{other}\:{solutions}\:{also}. \\ $$
Commented by Aina Samuel Temidayo last updated on 05/Sep/20
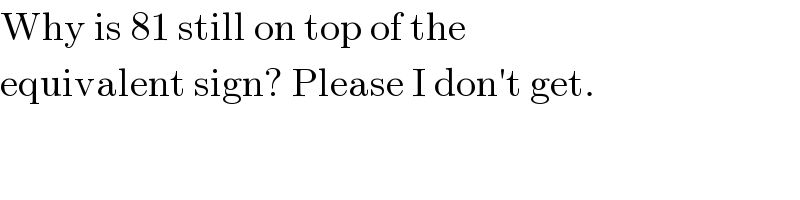
$$\mathrm{Why}\:\mathrm{is}\:\mathrm{81}\:\mathrm{still}\:\mathrm{on}\:\mathrm{top}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equivalent}\:\mathrm{sign}?\:\mathrm{Please}\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}. \\ $$
Commented by Aina Samuel Temidayo last updated on 05/Sep/20

$$\mathrm{Oh}.\:\mathrm{Ok}.\:\mathrm{Thanks}. \\ $$
Commented by Rasheed.Sindhi last updated on 05/Sep/20

$$@\:{Aina} \\ $$$${Sir}\:{Ahmadi}\:{has}\:{written} \\ $$$$\mathrm{79}{x}−\mathrm{81}{x}\overset{\mathrm{81}} {\equiv}−\mathrm{9}+{t} \\ $$$$\:\:\:\:\:{instead}\:{of} \\ $$$$\mathrm{79}{x}−\mathrm{81}{x}\equiv−\mathrm{9}+{t}\left({mod}\:\mathrm{81}\right) \\ $$$$ \\ $$
