Question Number 157126 by malwan last updated on 20/Oct/21
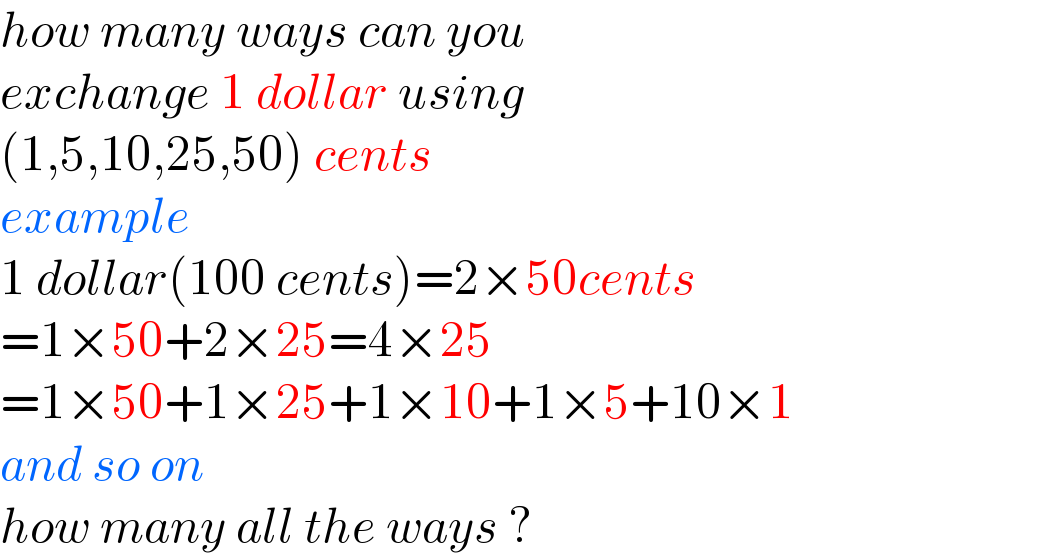
$${how}\:{many}\:{ways}\:{can}\:{you} \\ $$$${exchange}\:\mathrm{1}\:{dollar}\:{using} \\ $$$$\left(\mathrm{1},\mathrm{5},\mathrm{10},\mathrm{25},\mathrm{50}\right)\:{cents} \\ $$$${example} \\ $$$$\mathrm{1}\:{dollar}\left(\mathrm{100}\:{cents}\right)=\mathrm{2}×\mathrm{50}{cents} \\ $$$$=\mathrm{1}×\mathrm{50}+\mathrm{2}×\mathrm{25}=\mathrm{4}×\mathrm{25} \\ $$$$=\mathrm{1}×\mathrm{50}+\mathrm{1}×\mathrm{25}+\mathrm{1}×\mathrm{10}+\mathrm{1}×\mathrm{5}+\mathrm{10}×\mathrm{1} \\ $$$${and}\:{so}\:{on} \\ $$$${how}\:{many}\:{all}\:{the}\:{ways}\:? \\ $$
Commented by mr W last updated on 20/Oct/21
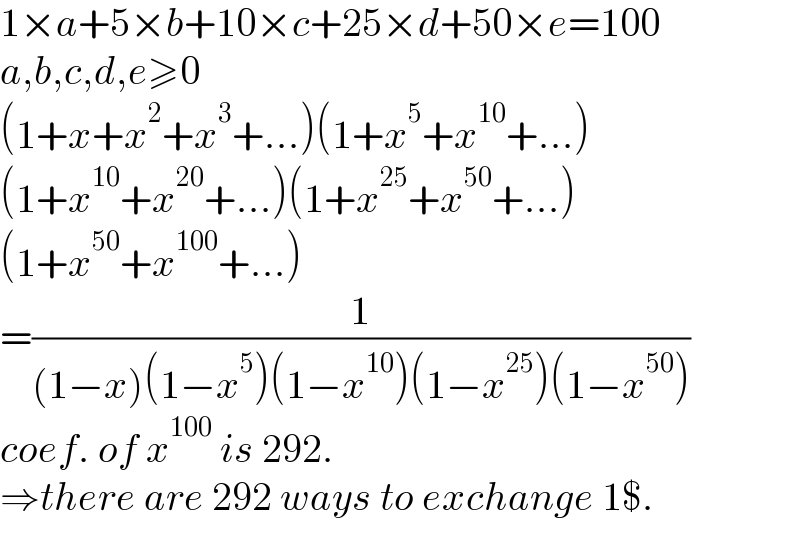
$$\mathrm{1}×{a}+\mathrm{5}×{b}+\mathrm{10}×{c}+\mathrm{25}×{d}+\mathrm{50}×{e}=\mathrm{100} \\ $$$${a},{b},{c},{d},{e}\geqslant\mathrm{0} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right)\left(\mathrm{1}+{x}^{\mathrm{5}} +{x}^{\mathrm{10}} +…\right) \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{10}} +{x}^{\mathrm{20}} +…\right)\left(\mathrm{1}+{x}^{\mathrm{25}} +{x}^{\mathrm{50}} +…\right) \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{50}} +{x}^{\mathrm{100}} +…\right) \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−{x}^{\mathrm{5}} \right)\left(\mathrm{1}−{x}^{\mathrm{10}} \right)\left(\mathrm{1}−{x}^{\mathrm{25}} \right)\left(\mathrm{1}−{x}^{\mathrm{50}} \right)} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{100}} \:{is}\:\mathrm{292}. \\ $$$$\Rightarrow{there}\:{are}\:\mathrm{292}\:{ways}\:{to}\:{exchange}\:\mathrm{1\$}. \\ $$
Commented by malwan last updated on 20/Oct/21

$${thank}\:{you}\:{sir} \\ $$
Commented by malwan last updated on 20/Oct/21

$${but}\:{I}\:{didnt}\:{understand}\:{how} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{100}} \:{is}\:\mathrm{292} \\ $$$${Can}\:{you}\:{please}\:{do}\:{more}\:{steps}? \\ $$$${thank}\:{you}\:{so}\:{much} \\ $$
Commented by mr W last updated on 20/Oct/21

$${in}\:{fact}\:{it}\:{is}\:{not}\:{easy}\:{to}\:{expand}\:{the} \\ $$$${generating}\:{function}\:{manuallly}.\:{i}\:{did} \\ $$$${let}\:{wolframalpha}\:{do}\:{it}. \\ $$
Commented by mr W last updated on 20/Oct/21

Commented by malwan last updated on 20/Oct/21
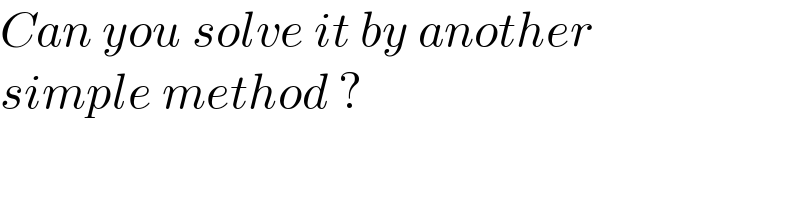
$${Can}\:{you}\:{solve}\:{it}\:{by}\:{another} \\ $$$${simple}\:{method}\:? \\ $$
Commented by mr W last updated on 20/Oct/21

Commented by mr W last updated on 20/Oct/21
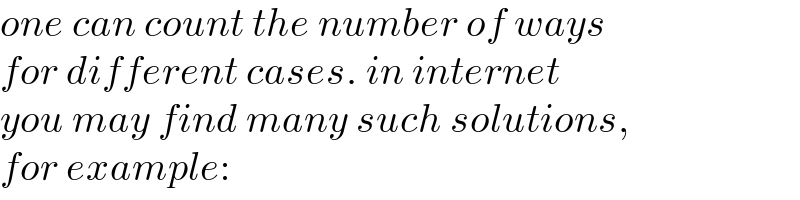
$${one}\:{can}\:{count}\:{the}\:{number}\:{of}\:{ways}\: \\ $$$${for}\:{different}\:{cases}.\:{in}\:{internet} \\ $$$${you}\:{may}\:{find}\:{many}\:{such}\:{solutions}, \\ $$$${for}\:{example}: \\ $$
Commented by Tawa11 last updated on 21/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
