Question Number 121851 by bemath last updated on 12/Nov/20

$${How}\:{many}\:{ways}\:{to}\:{arrange}\:{letters}\: \\ $$$${using}\:{letters}\:{in}\:{the}\:{word}\:{OKINKO} \\ $$$$\left({a}\right)\:\mathrm{1260}\:\:\:\:\:\left({b}\right)\:\mathrm{1160}\:\:\:\:\left({c}\right)\:\mathrm{980} \\ $$$$\left({d}\right)\:\mathrm{880}\:\:\:\:\:\:\:\:\left({e}\right)\:\mathrm{720} \\ $$
Commented by liberty last updated on 12/Nov/20
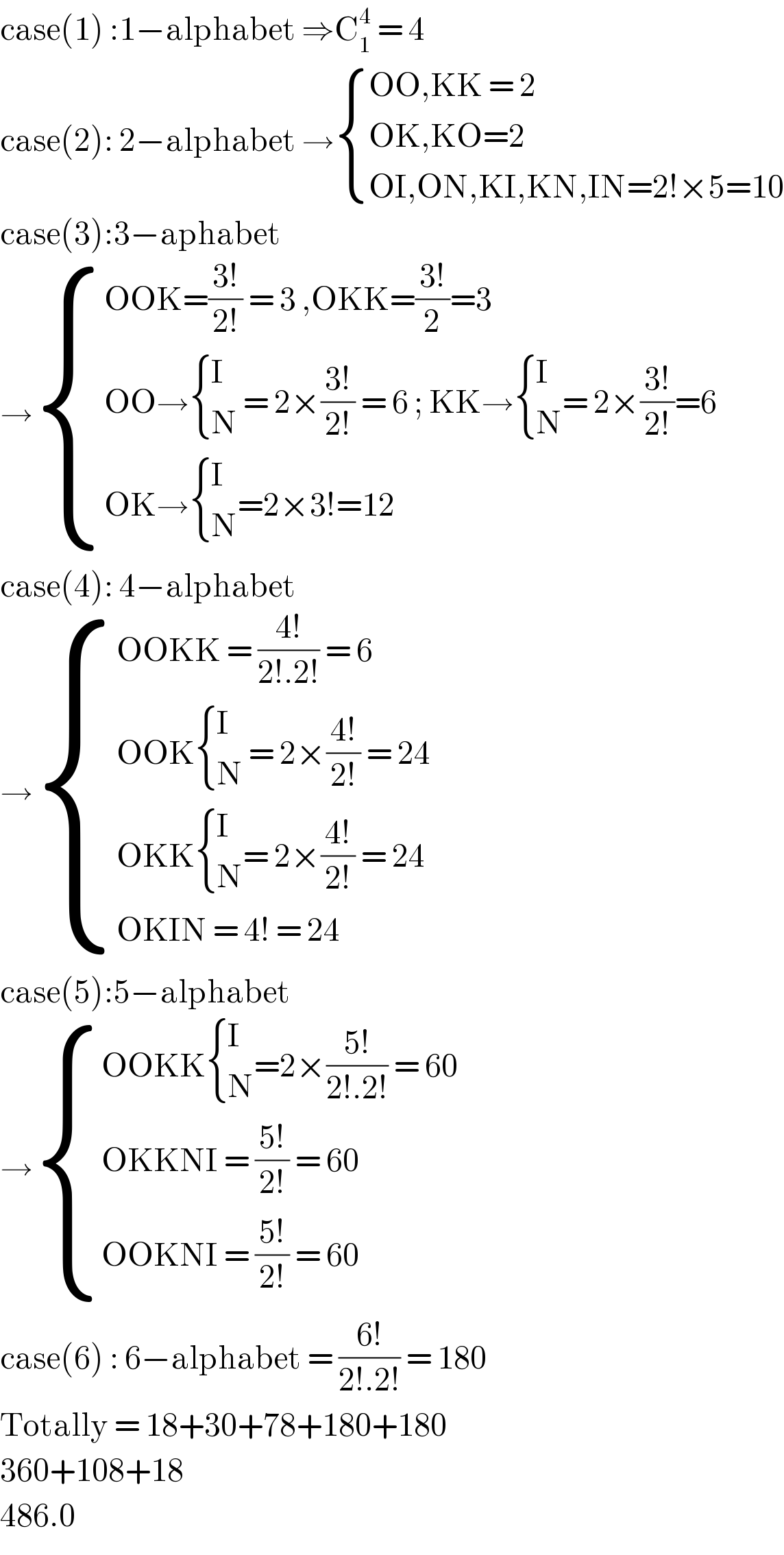
$$\mathrm{case}\left(\mathrm{1}\right)\::\mathrm{1}−\mathrm{alphabet}\:\Rightarrow\mathrm{C}_{\mathrm{1}} ^{\mathrm{4}} \:=\:\mathrm{4} \\ $$$$\mathrm{case}\left(\mathrm{2}\right):\:\mathrm{2}−\mathrm{alphabet}\:\rightarrow\begin{cases}{\mathrm{OO},\mathrm{KK}\:=\:\mathrm{2}}\\{\mathrm{OK},\mathrm{KO}=\mathrm{2}\:}\\{\mathrm{OI},\mathrm{ON},\mathrm{KI},\mathrm{KN},\mathrm{IN}=\mathrm{2}!×\mathrm{5}=\mathrm{10}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{3}\right):\mathrm{3}−\mathrm{aphabet} \\ $$$$\rightarrow\begin{cases}{\mathrm{OOK}=\frac{\mathrm{3}!}{\mathrm{2}!}\:=\:\mathrm{3}\:,\mathrm{OKK}=\frac{\mathrm{3}!}{\mathrm{2}}=\mathrm{3}}\\{\mathrm{OO}\rightarrow\begin{cases}{\mathrm{I}}\\{\mathrm{N}}\end{cases}\:=\:\mathrm{2}×\frac{\mathrm{3}!}{\mathrm{2}!}\:=\:\mathrm{6}\:;\:\mathrm{KK}\rightarrow\begin{cases}{\mathrm{I}}\\{\mathrm{N}}\end{cases}=\:\mathrm{2}×\frac{\mathrm{3}!}{\mathrm{2}!}=\mathrm{6}\:}\\{\mathrm{OK}\rightarrow\begin{cases}{\mathrm{I}}\\{\mathrm{N}}\end{cases}=\mathrm{2}×\mathrm{3}!=\mathrm{12}\:}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{4}\right):\:\mathrm{4}−\mathrm{alphabet} \\ $$$$\rightarrow\begin{cases}{\mathrm{OOKK}\:=\:\frac{\mathrm{4}!}{\mathrm{2}!.\mathrm{2}!}\:=\:\mathrm{6}\:}\\{\mathrm{OOK\begin{cases}{\mathrm{I}}\\{\mathrm{N}}\end{cases}}\:=\:\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{2}!}\:=\:\mathrm{24}\:}\\{\mathrm{OKK\begin{cases}{\mathrm{I}}\\{\mathrm{N}}\end{cases}}=\:\mathrm{2}×\frac{\mathrm{4}!}{\mathrm{2}!}\:=\:\mathrm{24}\:}\\{\mathrm{OKIN}\:=\:\mathrm{4}!\:=\:\mathrm{24}\:}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{5}\right):\mathrm{5}−\mathrm{alphabet} \\ $$$$\rightarrow\begin{cases}{\mathrm{OOKK\begin{cases}{\mathrm{I}}\\{\mathrm{N}}\end{cases}}=\mathrm{2}×\frac{\mathrm{5}!}{\mathrm{2}!.\mathrm{2}!}\:=\:\mathrm{60}}\\{\mathrm{OKKNI}\:=\:\frac{\mathrm{5}!}{\mathrm{2}!}\:=\:\mathrm{60}\:}\\{\mathrm{OOKNI}\:=\:\frac{\mathrm{5}!}{\mathrm{2}!}\:=\:\mathrm{60}\:}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{6}\right)\::\:\mathrm{6}−\mathrm{alphabet}\:=\:\frac{\mathrm{6}!}{\mathrm{2}!.\mathrm{2}!}\:=\:\mathrm{180} \\ $$$$\mathrm{Totally}\:=\:\mathrm{18}+\mathrm{30}+\mathrm{78}+\mathrm{180}+\mathrm{180} \\ $$$$\mathrm{360}+\mathrm{108}+\mathrm{18} \\ $$$$\mathrm{486}.\mathrm{0} \\ $$
