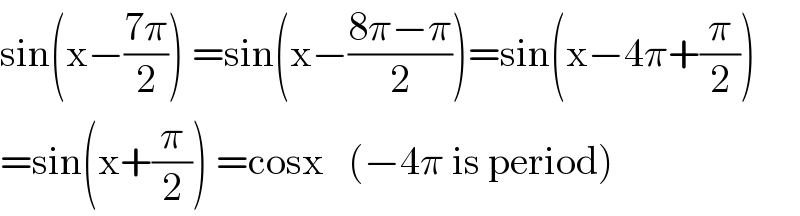Question Number 120244 by zahaku last updated on 30/Oct/20
$${how}\:{to}\:{justify}\:\:{that}\:\mathrm{sin}\:\left({x}−\frac{\mathrm{7}\pi}{\mathrm{2}}\:\right)=\:\mathrm{cos}\:{x} \\ $$
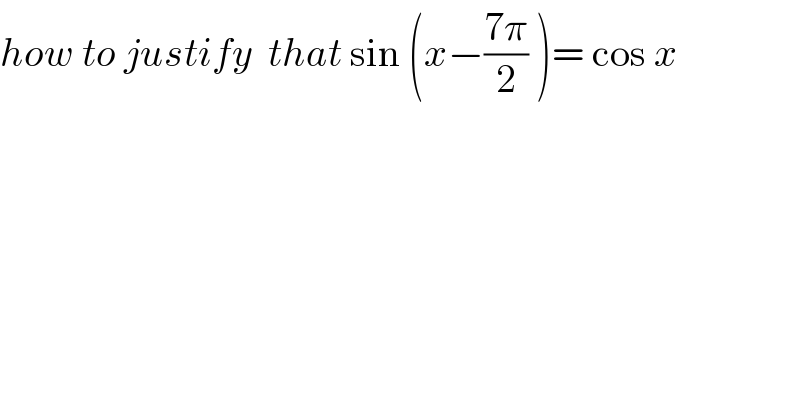
Commented by zahaku last updated on 30/Oct/20
$$\mathrm{sin}\:\left({x}−\frac{\mathrm{7}\pi}{\mathrm{2}}\:\right)=−\mathrm{sin}\:\left(\mathrm{2}\pi+\left({x}+\frac{\mathrm{3}\pi}{\mathrm{2}}\:\right)\:\:?\right. \\ $$
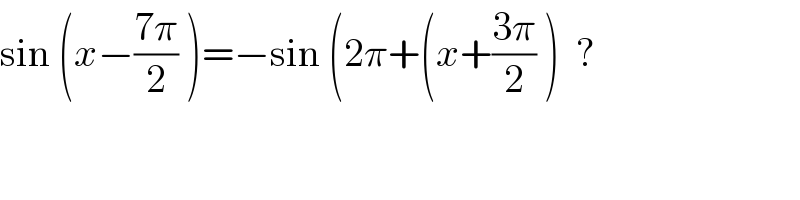
Commented by Aziztisffola last updated on 30/Oct/20
$$\frac{\mathrm{7}\pi}{\mathrm{2}}\equiv−\frac{\pi}{\mathrm{2}}\left(\mathrm{mod}\:\mathrm{2}\pi\right) \\ $$$${x}−\frac{\mathrm{7}\pi}{\mathrm{2}}\equiv\left({x}+\frac{\pi}{\mathrm{2}}\right)\left(\mathrm{mod}\:\mathrm{2}\pi\right) \\ $$$$\:\mathrm{sin}\left({x}+\frac{\pi}{\mathrm{2}}\right)=\mathrm{cos}\:{x} \\ $$
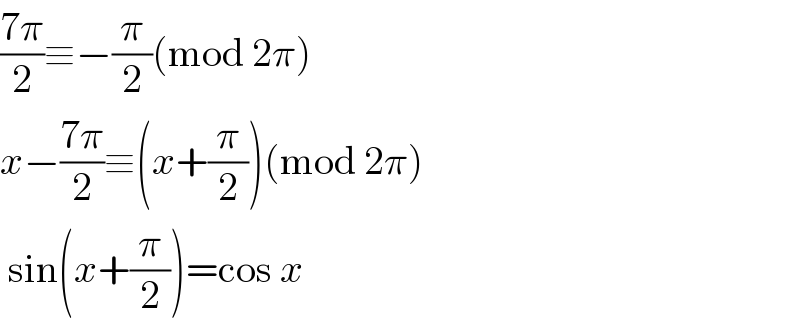
Answered by benjo_mathlover last updated on 30/Oct/20
![⇒sin (x−((7π)/2))=−sin (2π+(x+((3π)/2))) = −sin (x+((3π)/2)) =−[ sin (((3π)/2))cos x+cos (((3π)/2))sin x ] = −(−cos x+0)=cos x](https://www.tinkutara.com/question/Q120245.png)
$$\Rightarrow\mathrm{sin}\:\left({x}−\frac{\mathrm{7}\pi}{\mathrm{2}}\right)=−\mathrm{sin}\:\left(\mathrm{2}\pi+\left({x}+\frac{\mathrm{3}\pi}{\mathrm{2}}\right)\right) \\ $$$$=\:−\mathrm{sin}\:\left({x}+\frac{\mathrm{3}\pi}{\mathrm{2}}\right) \\ $$$$=−\left[\:\mathrm{sin}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)\mathrm{cos}\:{x}+\mathrm{cos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{2}}\right)\mathrm{sin}\:{x}\:\right] \\ $$$$=\:−\left(−\mathrm{cos}\:{x}+\mathrm{0}\right)=\mathrm{cos}\:{x} \\ $$
Answered by TANMAY PANACEA last updated on 30/Oct/20
![sin(x−((7π)/2)) =−sin(((7π)/2)−x) =−(−cosx) [here 7(odd number)×(π/2)−x ] lies in 4th quadrant so (−ve) sign =cosx](https://www.tinkutara.com/question/Q120250.png)
$${sin}\left({x}−\frac{\mathrm{7}\pi}{\mathrm{2}}\right) \\ $$$$=−{sin}\left(\frac{\mathrm{7}\pi}{\mathrm{2}}−{x}\right) \\ $$$$=−\left(−{cosx}\right)\:\:\left[{here}\:\mathrm{7}\left({odd}\:{number}\right)×\frac{\pi}{\mathrm{2}}−{x}\:\right]\:{lies}\:{in}\:\mathrm{4}{th}\:{quadrant}\:\:\boldsymbol{{so}}\:\left(−\boldsymbol{{ve}}\right)\:\boldsymbol{{sign}} \\ $$$$={cosx} \\ $$
Answered by mathmax by abdo last updated on 30/Oct/20
$$\mathrm{sin}\left(\mathrm{x}−\frac{\mathrm{7}\pi}{\mathrm{2}}\right)\:=\mathrm{sin}\left(\mathrm{x}−\frac{\mathrm{8}\pi−\pi}{\mathrm{2}}\right)=\mathrm{sin}\left(\mathrm{x}−\mathrm{4}\pi+\frac{\pi}{\mathrm{2}}\right) \\ $$$$=\mathrm{sin}\left(\mathrm{x}+\frac{\pi}{\mathrm{2}}\right)\:=\mathrm{cosx}\:\:\:\left(−\mathrm{4}\pi\:\mathrm{is}\:\mathrm{period}\right) \\ $$