how-to-prove-that-the-number-is-divisible-by-3-then-the-number-of-numbers-is-a-multiple-of-3-

Question Number 81647 by john santu last updated on 14/Feb/20

how to prove that the number

is divisible by 3, then the number

of numbers is a multiple of 3

Commented by mr W last updated on 14/Feb/20

d i d y o u w a n t t o s a y :

h o w t o p r o v e t h a t a n u m b e r i s d i v i s i b l e

b y 3 w h e n t h e s u m o f i t s d i g i t s i s a

m u l t i p l e o f 3 .

o r

h o w t o p r o v e t h a t, i f a n u m b e r i s d i v i s i b l e

b y 3, t h e n t h e s u m o f i t s d i g i t s i s a

m u l t i p l e o f 3 .

Commented by Kunal12588 last updated on 14/Feb/20

100 a + 10 b + c = 3 q f o r a 3 d i g i t n o .

\Rightarrow 3 q = 99 a + 9 b + (a + b + c)

\Rightarrow q = 33 a + 3 b + \frac{a + b + c}{3}

q \in N \Rightarrow a + b + c ∣ 3

f o r a^{'} n^{'} d i g i t n o .

3 m = \underset{i = 0}{\sum^{n - 1}} 10^{i} a_{i}; a_{i} i s {(i + 1)}^{t h} d i g i t

\Rightarrow m = 3 k + \frac{1}{3} \underset{i = 0}{\sum^{n - 1}} a_{i}

\Rightarrow \underset{i = 0}{\sum^{n - 1}} a_{i} i s d i v i s i b l e b y 3 .

p l e a s e h e l p m e t o f i n d k

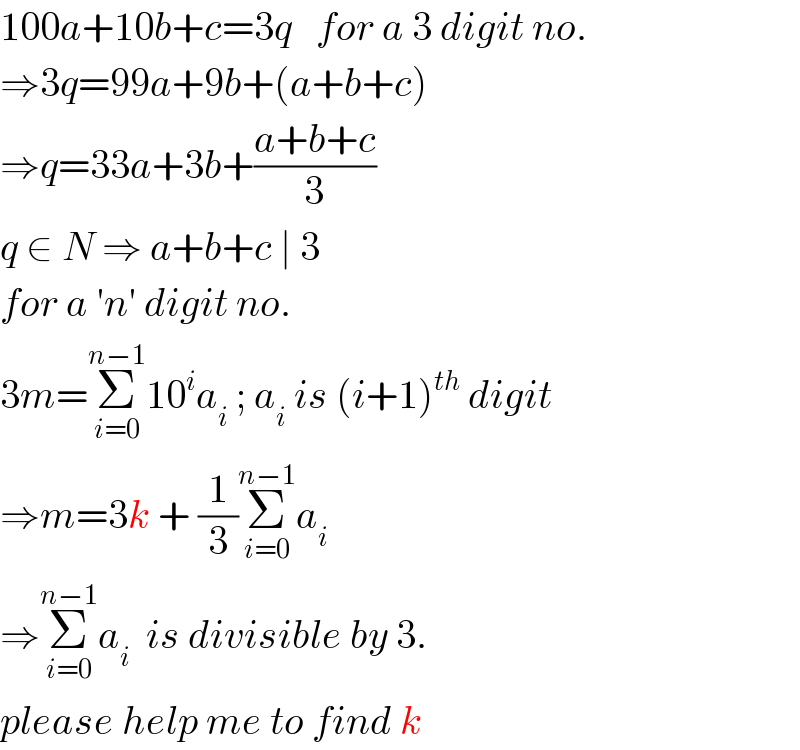
Commented by Prithwish Sen 1 last updated on 14/Feb/20

a n y n u m b e r c a n b e r e p r e s e n t e d b y

N = 10^{n} x_{n} + 10^{n - 1} x_{n - 1} + \dots \dots . . + 10^{2} x_{2} + 10 x_{1} + x_{0}

n o w

x_{n} + x_{n - 1} + \dots \dots \dots . . + x_{1} + x_{0} = 3 k

∴ N = (999 \dots n t i m e s + 1) x_{n} + \dots \dots + (99 + 1) x_{2} + (9 + 1) x_{1} + x_{0}

= (999 \dots n t i m e s . x_{n} + \dots . + 99 x_{2} + 9 x_{1}) + (x_{n} + x_{n - 1} + \dots . . + x_{2} + x_{1} + x_{0})

= 3 m + 3 k

i . e N i s a l s o d i v i s i b l e b y 3 (p r o v e d)

Commented by mr W last updated on 14/Feb/20

3 m = \underset{i = 0}{\sum^{n - 1}} 10^{i} a_{i}

3 m = \underset{i = 0}{\sum^{n - 1}} {(1 + 9)}^{i} a_{i}

3 m = \underset{i = 0}{\sum^{n - 1}} [\underset{k = 0}{\sum^{i}} C_{k}^{i} 9^{k}] a_{i}

3 m = \underset{i = 0}{\sum^{n - 1}} [1 + \underset{k = 1}{\sum^{i}} C_{k}^{i} 9^{k}] a_{i}

3 m = \underset{i = 0}{\sum^{n - 1}} a_{i} + \underset{i = 1}{\sum^{n - 1}} (\underset{k = 1}{\sum^{i}} C_{k}^{i} 3^{2 k}) a_{i}

3 m = \underset{i = 0}{\sum^{n - 1}} a_{i} + 3 h

\Rightarrow \underset{i = 0}{\sum^{n - 1}} a_{i} = 3 (m - h) = m u l t i p l e o f 3

Commented by Prithwish Sen 1 last updated on 14/Feb/20

H o w a r e y o u s i r ?

Commented by mr W last updated on 14/Feb/20

e v e r y t h i n g i s o k w i t h m e, t h a n k s!

y o u t o o s i r ?

Commented by john santu last updated on 14/Feb/20

yes .

Commented by Prithwish Sen 1 last updated on 15/Feb/20

f i n e s i r .