Question Number 56092 by Mikael_Marshall last updated on 10/Mar/19
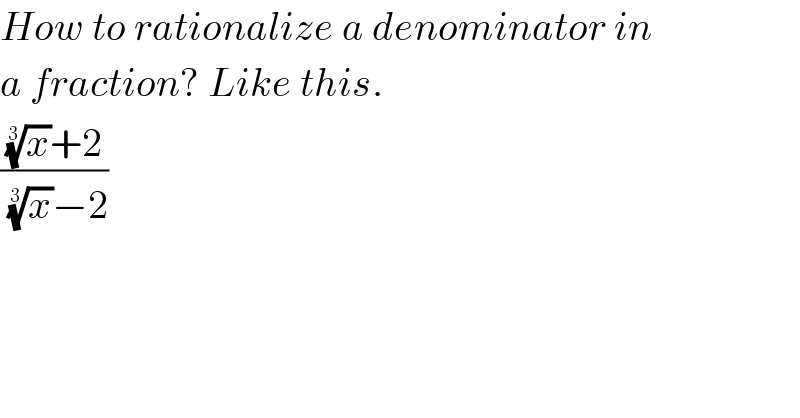
$${How}\:{to}\:{rationalize}\:{a}\:{denominator}\:{in} \\ $$$${a}\:{fraction}?\:{Like}\:{this}. \\ $$$$\frac{\sqrt[{\mathrm{3}}]{{x}}+\mathrm{2}}{\:\sqrt[{\mathrm{3}}]{{x}}−\mathrm{2}}\: \\ $$
Answered by math1967 last updated on 10/Mar/19
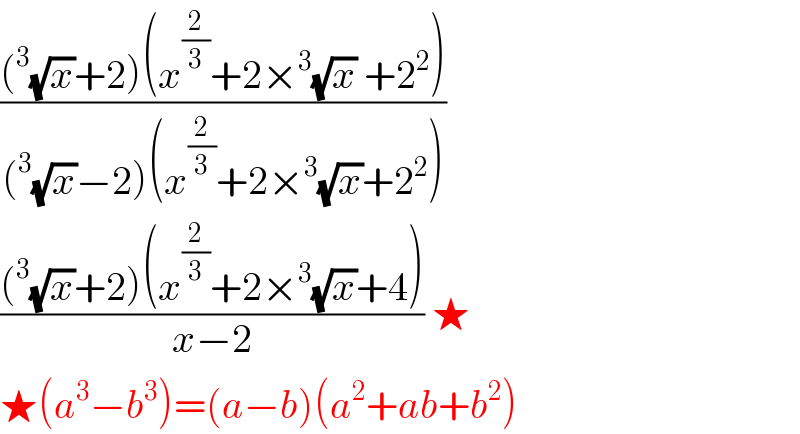
$$\frac{\left(^{\mathrm{3}} \sqrt{{x}}+\mathrm{2}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{2}×^{\mathrm{3}} \sqrt{{x}}\:+\mathrm{2}^{\mathrm{2}} \right)}{\left(^{\mathrm{3}} \sqrt{{x}}−\mathrm{2}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{2}×^{\mathrm{3}} \sqrt{{x}}+\mathrm{2}^{\mathrm{2}} \right)}\:\:\: \\ $$$$\frac{\left(^{\mathrm{3}} \sqrt{{x}}+\mathrm{2}\right)\left({x}^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{2}×^{\mathrm{3}} \sqrt{{x}}+\mathrm{4}\right)}{{x}−\mathrm{2}}\:\bigstar \\ $$$$\bigstar\left({a}^{\mathrm{3}} −{b}^{\mathrm{3}} \right)=\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right) \\ $$
Commented by Mikael_Marshall last updated on 10/Mar/19

$${thanks}\:{Sir} \\ $$
Answered by peter frank last updated on 10/Mar/19
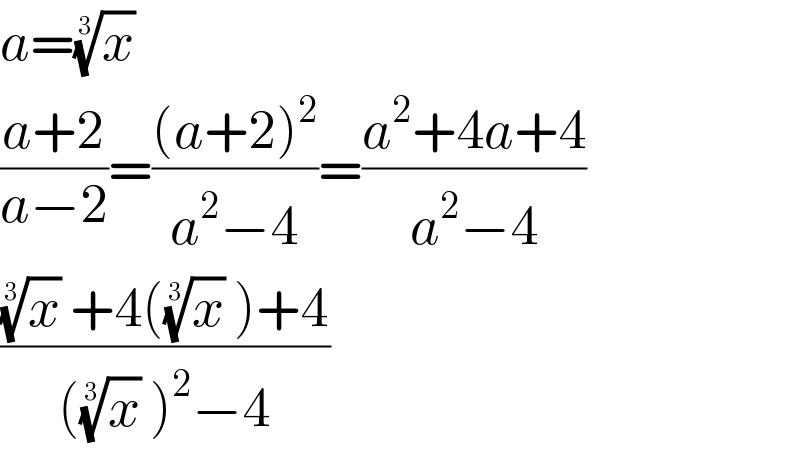
$${a}=\sqrt[{\mathrm{3}}]{{x}} \\ $$$$\frac{{a}+\mathrm{2}}{{a}−\mathrm{2}}=\frac{\left({a}+\mathrm{2}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} −\mathrm{4}}=\frac{{a}^{\mathrm{2}} +\mathrm{4}{a}+\mathrm{4}}{{a}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\frac{\sqrt[{\mathrm{3}}]{{x}}\:+\mathrm{4}\left(\sqrt[{\mathrm{3}}]{{x}}\:\right)+\mathrm{4}}{\left(\sqrt[{\mathrm{3}}]{{x}}\:\right)^{\mathrm{2}} −\mathrm{4}}\: \\ $$
Commented by math1967 last updated on 10/Mar/19
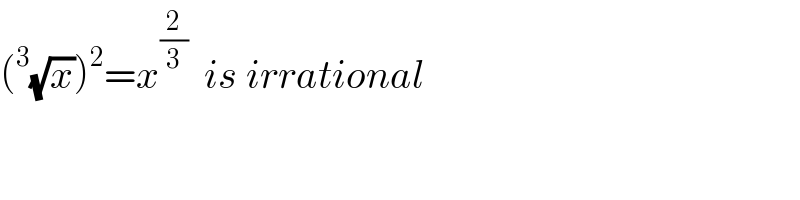
$$\left(^{\mathrm{3}} \sqrt{{x}}\right)^{\mathrm{2}} ={x}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\:{is}\:{irrational} \\ $$
