Question Number 87224 by jagoll last updated on 03/Apr/20
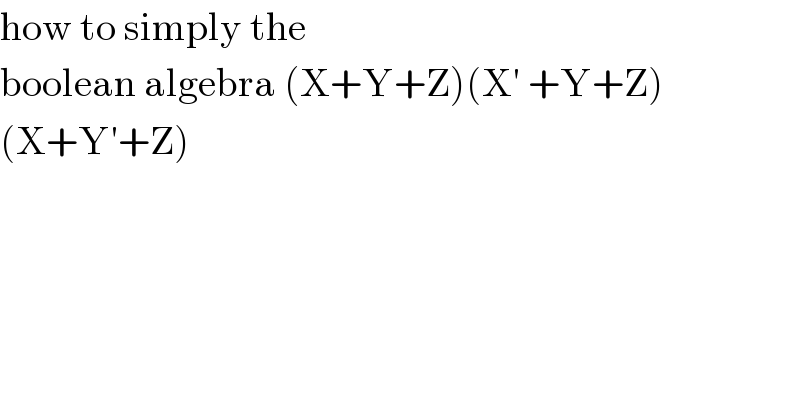
$$\mathrm{how}\:\mathrm{to}\:\mathrm{simply}\:\mathrm{the}\: \\ $$$$\mathrm{boolean}\:\mathrm{algebra}\:\left(\mathrm{X}+\mathrm{Y}+\mathrm{Z}\right)\left(\mathrm{X}'\:+\mathrm{Y}+\mathrm{Z}\right) \\ $$$$\left(\mathrm{X}+\mathrm{Y}'+\mathrm{Z}\right)\: \\ $$
Commented by jagoll last updated on 03/Apr/20

$$\mathrm{how}\:\mathrm{sir}? \\ $$
Commented by redmiiuser last updated on 03/Apr/20

$${is}\:{it}\:{correct}? \\ $$
Commented by john santu last updated on 03/Apr/20
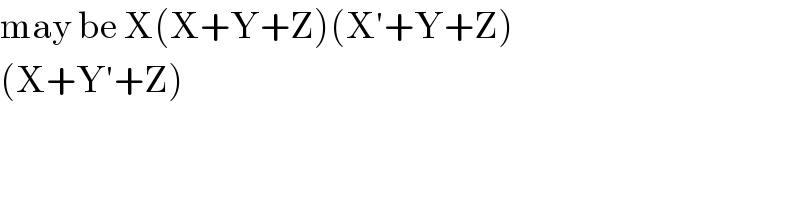
$$\mathrm{may}\:\mathrm{be}\:\mathrm{X}\left(\mathrm{X}+\mathrm{Y}+\mathrm{Z}\right)\left(\mathrm{X}'+\mathrm{Y}+\mathrm{Z}\right) \\ $$$$\left(\mathrm{X}+\mathrm{Y}'+\mathrm{Z}\right)\: \\ $$
Commented by redmiiuser last updated on 03/Apr/20
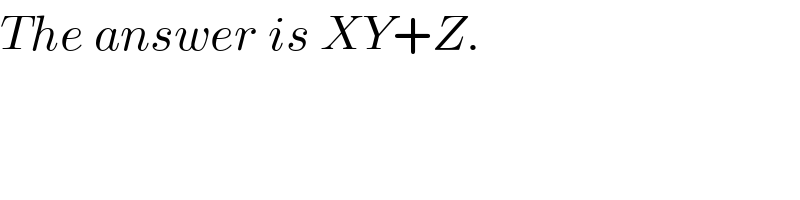
$${The}\:{answer}\:{is}\:{XY}+{Z}. \\ $$
Commented by redmiiuser last updated on 03/Apr/20
$${PLS}\:{CHECK} \\ $$
Commented by jagoll last updated on 03/Apr/20

$$\mathrm{yes} \\ $$
Commented by redmiiuser last updated on 03/Apr/20
$${ok}\:{i}\:{will}\:{post}\:{my}\:{work}. \\ $$
Answered by redmiiuser last updated on 03/Apr/20
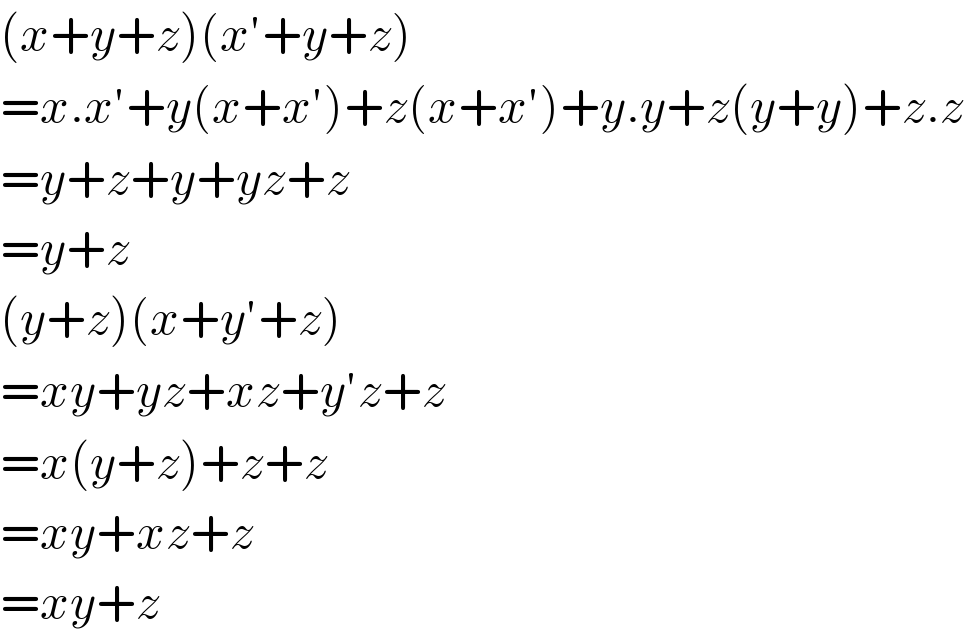
$$\left({x}+{y}+{z}\right)\left({x}'+{y}+{z}\right) \\ $$$$={x}.{x}'+{y}\left({x}+{x}'\right)+{z}\left({x}+{x}'\right)+{y}.{y}+{z}\left({y}+{y}\right)+{z}.{z} \\ $$$$={y}+{z}+{y}+{yz}+{z} \\ $$$$={y}+{z} \\ $$$$\left({y}+{z}\right)\left({x}+{y}'+{z}\right) \\ $$$$={xy}+{yz}+{xz}+{y}'{z}+{z} \\ $$$$={x}\left({y}+{z}\right)+{z}+{z} \\ $$$$={xy}+{xz}+{z} \\ $$$$={xy}+{z} \\ $$
