Question Number 148809 by jlewis last updated on 31/Jul/21
![Σ_(i=0) ^∞ [(−0.5x^2 )i/i!] integrate](https://www.tinkutara.com/question/Q148809.png)
$$\underset{\mathrm{i}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\left(−\mathrm{0}.\mathrm{5x}^{\mathrm{2}} \right)\mathrm{i}/\mathrm{i}!\right]\:\mathrm{integrate} \\ $$
Answered by qaz last updated on 31/Jul/21
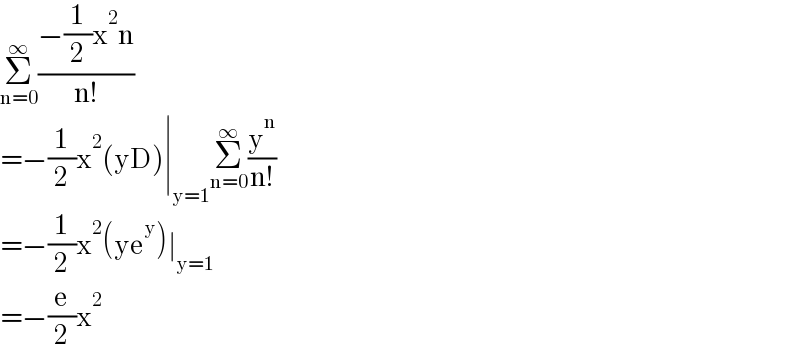
$$\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \mathrm{n}}{\mathrm{n}!} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \left(\mathrm{yD}\right)\mid_{\mathrm{y}=\mathrm{1}} \underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{y}^{\mathrm{n}} }{\mathrm{n}!} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \left(\mathrm{ye}^{\mathrm{y}} \right)\mid_{\mathrm{y}=\mathrm{1}} \\ $$$$=−\frac{\mathrm{e}}{\mathrm{2}}\mathrm{x}^{\mathrm{2}} \\ $$
