Menu Close

I-0-1-Li-2-x-1-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 164585 by mnjuly1970 last updated on 19/Jan/22
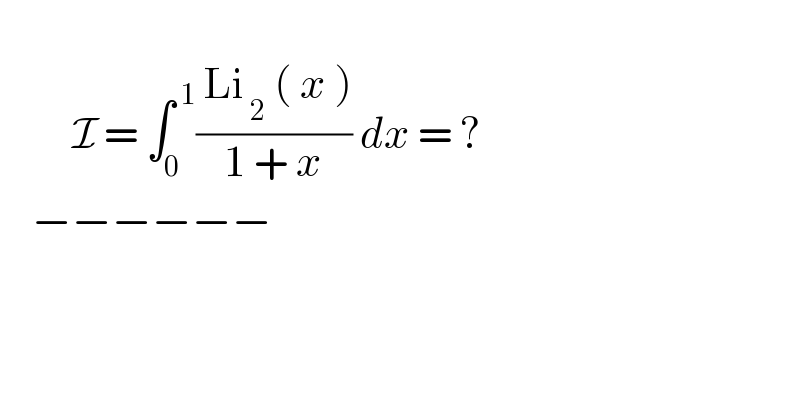
I = ∫_0 ^( 1) (( Li_( 2) ( x ))/(1 + x)) dx = ? −−−−−−
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\mathcal{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\mathrm{Li}_{\:\mathrm{2}} \:\left(\:{x}\:\right)}{\mathrm{1}\:+\:{x}}\:{dx}\:=\:? \\ $$$$\:\:\:\:−−−−−−\: \\ $$
Answered by mindispower last updated on 19/Jan/22
∫_0 ^1 ((Li_2 (x))/(1+x))dx=ln(2)(π^2 /6)+∫_0 ^1 ((ln(1−x)ln(1+x))/x)dx_(=A) A=(1/4)∫_0 ^1 ((ln^2 (1−x^2 ))/x)−((ln^2 (((1−x)/(1+x))))/x)dx =(1/8)∫_0 ^1 ((ln^2 (1−y))/y)dy−(1/2)∫_0 ^1 ((ln^2 (y))/(1−y^2 ))dy =(1/8)∫_0 ^∞ ((t^2 e^(−t) )/(1−e^(−t) )) −(1/2)∫_0 ^∞ ((t^2 e^(−t) )/(1−e^(−2t) ))dt =(1/8)Γ(3)ζ(3)−(1/2)Σ_(n≥0) ∫_0 ^∞ t^2 e^(−(1+2n)t) dt =((𝛇(3))/4)−Σ_(n≥0) ((Γ(3))/(2(2n+1)^3 )) =((ζ(3))/4)−(7/8)ζ(3)=−(5/8)ζ(3) ∫_0 ^1 ((Li_2 (x))/(1+x))dx=((ln(2))/6)π^2 −(5/8)ζ(3)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Li}_{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx}={ln}\left(\mathrm{2}\right)\frac{\pi^{\mathrm{2}} }{\mathrm{6}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right){ln}\left(\mathrm{1}+{x}\right)}{{x}}{dx}_{={A}} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{{x}}−\frac{{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\right)}{{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left(\mathrm{1}−{y}\right)}{{y}}{dy}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({y}\right)}{\mathrm{1}−{y}^{\mathrm{2}} }{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} {e}^{−{t}} }{\mathrm{1}−{e}^{−{t}} }\:−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\mathrm{2}} {e}^{−{t}} }{\mathrm{1}−{e}^{−\mathrm{2}{t}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\Gamma\left(\mathrm{3}\right)\zeta\left(\mathrm{3}\right)−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\geqslant\mathrm{0}} {\sum}\int_{\mathrm{0}} ^{\infty} {t}^{\mathrm{2}} {e}^{−\left(\mathrm{1}+\mathrm{2}\boldsymbol{{n}}\right)\boldsymbol{{t}}} \boldsymbol{{dt}} \\ $$$$=\frac{\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{4}}−\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\Gamma\left(\mathrm{3}\right)}{\mathrm{2}\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{\zeta\left(\mathrm{3}\right)}{\mathrm{4}}−\frac{\mathrm{7}}{\mathrm{8}}\zeta\left(\mathrm{3}\right)=−\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Li}_{\mathrm{2}} \left({x}\right)}{\mathrm{1}+{x}}{dx}=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{6}}\pi^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{8}}\zeta\left(\mathrm{3}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 19/Jan/22
thank hou so much sir power . very nice solution..
$$\:\:\:\:{thank}\:{hou}\:{so}\:{much}\:{sir}\:{power} \\ $$$$.\:{very}\:{nice}\:{solution}..\: \\ $$$$\:\:\: \\ $$
Commented by mindispower last updated on 19/Jan/22
Withe Pleasur Have a nice Day sir
$${Withe}\:{Pleasur}\:{Have}\:{a}\:{nice}\:{Day}\:{sir} \\ $$
Answered by Lordose last updated on 19/Jan/22
I = ∫_0 ^( 1) ((Li_2 (x))/(1+x))dx I =^(IBP) Li_2 (x)ln(1+x)∣_0 ^1 + ∫_0 ^( 1) ((ln(1−x)ln(1+x))/x)dx I = ln(2)𝛇(2) + ∫_0 ^( 1) ((ln(1−x)ln(1+x))/x)dx J = −(1/2)(∫_0 ^( 1) ln^2 (((1−x)/(1+x)))(dx/x) − ∫_0 ^( 1) ((ln^2 (1−x))/x)dx −∫_0 ^( 1) ((ln^2 (1+x))/x)dx) J =−(1/2)(A − B − C) A =^(x=((1−x)/(1+x))) 2∫_0 ^( 1) ((ln^2 (x))/(1−x^2 ))dx = 2Σ_(k=0) ^∞ ∫_0 ^( 1) x^(2k) ln^2 (x)dx A =^(IBP×2) 4Σ_(k=0) ^∞ (1/((2k+1)^3 )) = 4(((7𝛇(3))/8)) = ((7𝛇(3))/2) A = ((7𝛇(3))/2) B =^(x=1−x) ∫_0 ^( 1) ((ln^2 (x))/(1−x))dx = Σ_(k=1) ^∞ ∫_0 ^( 1) x^(k−1) ln^2 (x)dx B =^(IBP×2) 2Σ_(k=1) ^∞ (1/k^3 ) = 2𝛇(3) B = 2𝛇(3) C = (1/4)𝛇(3) J = −(1/2)(((7𝛇(3))/2) − 2𝛇(3) − ((𝛇(3))/4)) = −((5𝛇(3))/8) I = ln(2)𝛇(2) + ((5𝛇(3))/8) I = 𝛇(2)ln(2) + ((5𝛇(3))/8)
$$ \\ $$$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{I}\:\overset{\boldsymbol{\mathrm{IBP}}} {=}\mathrm{Li}_{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{I}\:=\:\mathrm{ln}\left(\mathrm{2}\right)\boldsymbol{\zeta}\left(\mathrm{2}\right)\:+\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\: \\ $$$$\mathrm{J}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}\right)\frac{\mathrm{dx}}{\mathrm{x}}\:−\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:−\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\right) \\ $$$$\mathrm{J}\:=−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{A}\:−\:\mathrm{B}\:−\:\mathrm{C}\right) \\ $$$$\mathrm{A}\:\overset{\mathrm{x}=\frac{\mathrm{1}−\mathrm{x}}{\mathrm{1}+\mathrm{x}}} {=}\mathrm{2}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:=\:\mathrm{2}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{2k}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{A}\:\overset{\boldsymbol{\mathrm{IBP}}×\mathrm{2}} {=}\:\mathrm{4}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2k}+\mathrm{1}\right)^{\mathrm{3}} }\:=\:\mathrm{4}\left(\frac{\mathrm{7}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{8}}\right)\:=\:\frac{\mathrm{7}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{2}} \\ $$$$\boldsymbol{\mathrm{A}}\:=\:\frac{\mathrm{7}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{2}} \\ $$$$\mathrm{B}\:\overset{\mathrm{x}=\mathrm{1}−\mathrm{x}} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:=\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \mathrm{x}^{\mathrm{k}−\mathrm{1}} \mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{B}\:\overset{\boldsymbol{\mathrm{IBP}}×\mathrm{2}} {=}\:\mathrm{2}\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{k}^{\mathrm{3}} }\:=\:\mathrm{2}\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$$$\boldsymbol{\mathrm{B}}\:=\:\mathrm{2}\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$$$\mathrm{C}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\boldsymbol{\zeta}\left(\mathrm{3}\right) \\ $$$$\mathrm{J}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{7}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{2}}\:−\:\mathrm{2}\boldsymbol{\zeta}\left(\mathrm{3}\right)\:−\:\frac{\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{4}}\right)\:=\:−\frac{\mathrm{5}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$\mathrm{I}\:=\:\mathrm{ln}\left(\mathrm{2}\right)\boldsymbol{\zeta}\left(\mathrm{2}\right)\:+\:\frac{\mathrm{5}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$$$\boldsymbol{\mathrm{I}}\:=\:\boldsymbol{\zeta}\left(\mathrm{2}\right)\boldsymbol{\mathrm{ln}}\left(\mathrm{2}\right)\:+\:\frac{\mathrm{5}\boldsymbol{\zeta}\left(\mathrm{3}\right)}{\mathrm{8}} \\ $$
Commented by mnjuly1970 last updated on 19/Jan/22
thx a lot sir lordos
$$\:\:{thx}\:{a}\:{lot}\:{sir}\:{lordos} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *